题目内容
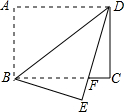如图，在长方形ABCD中，AB∥CD，AD∥BC，AB=3，BC=4，将矩形纸片沿BD折叠，使点A落在点E处．设DE与BC相交于点F，（1）判断△BDF的形状，并说明理由；
（2）求DF的长．
考点：翻折变换（折叠问题）
专题：
分析：（1）利用翻折变换的性质及矩形的性质证明BF=DF即可解决问题．
（2）利用勾股定理列出关于线段DF的方程即可解决问题．
（2）利用勾股定理列出关于线段DF的方程即可解决问题．
解答：解：（1）
由题意得：△ABD≌△EBD，
∴∠ADB=∠FDB；
又∵四边形ABCD为长方形，
∴AD∥BC，
∴∠ADB=∠DBF，
∴∠FDB=∠DBF，
∴BF=DF，
∴△BDF为等腰三角形．
（2）
由（1）知：DC=AB=3，
BF=DF（设为x），
则CF=4-x；
由勾股定理得：x2=（4-x）2+32，
解得：x=
，
即DF的长为
．
解：（1）由题意得：△ABD≌△EBD，
∴∠ADB=∠FDB；
又∵四边形ABCD为长方形，
∴AD∥BC，
∴∠ADB=∠DBF，
∴∠FDB=∠DBF，
∴BF=DF，
∴△BDF为等腰三角形．
（2）
由（1）知：DC=AB=3，
BF=DF（设为x），
则CF=4-x；
由勾股定理得：x2=（4-x）2+32，
解得：x=
| 25 |
| 8 |
即DF的长为
| 25 |
| 8 |
点评：该命题主要考查了翻折变换的性质及其应用的问题；解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
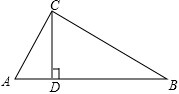已知在△ABC中，CD⊥AB于D，由下列条件中的某一个就能推出△ABC是直角三角形的是
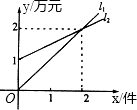如图，l1表示某公司一种产品一天的销售收入与销售量的关系，l2表示该公司这种产品一天的销售成本与销售量的关系．