题目内容
2.某工厂生产的某种产品按质量分为10个档次,第1档次(最低档次)的产品一天能生产95件,每件利润6元.每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次;
(3)求该产品一天的总利润为y的最大值.
分析 (1)由题意得出第x档次提高的档次是x-1档,根据总利润=单件利润×产量可得函数解析式;
(2)根据题意列出关于x的一元二次方程,解方程求得x的值,结合x的范围取舍即可得;
(3)将函数解析式配方成顶点式即可得最值情况.
解答 解:(1)∵第一档次的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润加2元,但一天生产量减少5件.
∴第x档次,提高的档次是x-1档.
∴y=[6+2(x-1)][95-5(x-1)],
即y=-10x2+180x+400(其中x是正整数,且1≤x≤10);
(2)由题意可得:-10x2+180x+400=1120
整理得:x2-18x+72=0
解得:x1=6,x2=12(舍去).
答:该产品的质量档次为第6档.
(3)∵y=-10x2+180x+400=-10(x-9)2+1210
∴该产品一天的总利润为y的最大值=1210元.
点评 本题主要考查二次函数的应用和一元二次方程的应用,根据相等关系列出函数解析式及一元二次方程是解题的关键.

练习册系列答案
相关题目
13.下列实数中的无理数是( )
| A. | π | B. | $\frac{1}{2}$ | C. | 0.62626262 | D. | -8 |
10.若点(a,6)关于原点的对称点是(-5,b),则a+b的值为( )
| A. | 1 | B. | -1 | C. | 11 | D. | -11 |
17.抛物线y=x2+bx+c与x轴的交点A(x1,0),B(x2,0)(x1<x2),一元二次方程x2+bx+c-1=0的两根为m,n(m<n),则下列说法错误的是( )
| A. | b2>4c | B. | x1+x2>m+n | C. | x1x2>mn | D. | m<x1<x2<n |
7.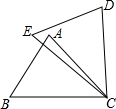 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
 如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )
如图,在△ABC和△DEC中,已知BC=EC,∠B=∠E,还需添加一个条件才能使△ABC≌△DEC,不能添加的一个条件是( )| A. | ∠BCE=∠ACD | B. | AC=DC | C. | ∠A=∠D | D. | AB=DE |
11.下列各式正确的是( )
| A. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$÷$\sqrt{3}$=$\frac{\sqrt{6}}{3}$ | D. | 5$\sqrt{5}$-2$\sqrt{2}$=3$\sqrt{3}$ |
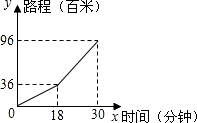 小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟.
小明早晨从进学校骑车到学校,先上坡后下坡,行程情况如图所示,若返回时上坡、下坡的速度和原来相同,那么小亮从学校骑车回家用的时间是37.2分钟.