题目内容
5．
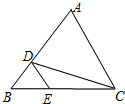如图，在△ABC中，D、E分别是AB、BC上的点，且DE∥AC，若S△BDE：S△BAC=1：9，则 S△BDE：S△CDE=1：2．
分析 由DE∥AC，得到△BDE∽△ABC，根据相似三角形的性质得到S△BDE：S△BAC=${（\frac{BE}{BC}）}^{2}$=$\frac{1}{9}$，根据$\frac{BE}{CE}$=$\frac{1}{2}$，得到S△BDE：S△CDE=$\frac{BE}{BC}$=$\frac{1}{2}$．
解答 解：∵DE∥AC，
∴△BDE∽△ABC，
∴S△BDE：S△BAC=${（\frac{BE}{BC}）}^{2}$=$\frac{1}{9}$，
∴$\frac{BE}{BC}$=$\frac{1}{3}$，
∴$\frac{BE}{CE}$=$\frac{1}{2}$，
∴S△BDE：S△CDE=$\frac{BE}{BC}$=$\frac{1}{2}$．
故答案为：1：2．
点评 本题考查了相似三角形的判定与性质，等高的三角形的面积的比等于底边的比，熟记相似三角形面积的比等于相似比的平方，用△BDE的面积表示出△ABC的面积是解题的关键．
练习册系列答案
相关题目
如图，在?ABCD中，∠ADC的角平分线DE交AC于点F，AE=2，则AD=2．
16．下列各数中，比-2大的数是（ ）
| A． | -3 | B． | 0 | C． | -2 | D． | -2.1 |
13．下列命题正确的个数是（ ）
①一组对角相等，一组对边平行的四边形是平行四边形；
②有两条边和第三条边上的中线对应相等的两个三角形全等；
③对角线垂直相等的四边形是正方形；
④圆的切线垂直于圆的半径．
①一组对角相等，一组对边平行的四边形是平行四边形；
②有两条边和第三条边上的中线对应相等的两个三角形全等；
③对角线垂直相等的四边形是正方形；
④圆的切线垂直于圆的半径．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
如图，一块平行四边形场地ABCD，测得∠ABC=60°，AB=2，AD=4，AE⊥BD于点E，CF⊥BD于点F，连接CE，AF．现计划在四边形AECF区域内种植花草．
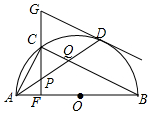如图，在⊙O中，AB是直径，点D是⊙O上一点，点C是弧AD的中点，弦CF⊥AB于点E，过点D的切线交FC的延长线于点G，连接AD，分别交CF、CB于点P、Q，连接AC．给出下列结论：①∠BAD=∠ABC；②AD=CB；③点P是△ACQ的外心；④GP=GD；⑤CB∥GD．其中正确结论的序号是（ ）
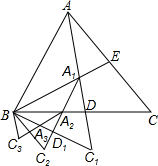已知如图，△ABC是面积为1的正三角形，AC和BC两边上的高BE与AD相交于点A1，延长AD到C1，使C1D=A1D，连接BC1，得△A1BC1，作其BC1边上的高A1D1交BD于A2，延长A1D1到C2，使A2D1=C2D1，连接BC2，得△A2BC2，有同样的方法得△A3BC3…当AnB与AB第一次重合时，△AnBCn的面积是$\frac{1}{{3}^{12}}$．