题目内容
10.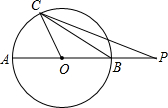 如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.
如图,AB是⊙O的直径,延长OB至P,使BP=OB,点C为圆上除A、B外的任一点.设∠PCB=α,∠POC=β.则tanα•tan$\frac{β}{2}$的值为$\frac{1}{3}$.
分析 首先过点B作BD⊥BC,垂足为B,交CP于点D,连接AC,易证得BD∥AC,证得△PBD∽△PAC,然后由相似三角形的对应边成比例,求得BD:AC的值,又由tan$\frac{1}{2}$β=$\frac{BC}{AC}$,tanα=$\frac{BD}{BC}$,即可求得答案.
解答 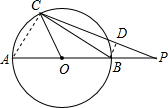 解:过点B作BD⊥BC,垂足为B,交CP于点D,连接AC,
解:过点B作BD⊥BC,垂足为B,交CP于点D,连接AC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴AC∥BD,
∴△PBD∽△PAC,
∴BD:AC=PB:PA,
∵BP=OB,OA=OB,
∴$\frac{BD}{AC}$=$\frac{BP}{AP}$=$\frac{1}{3}$;
∵∠A=$\frac{1}{2}$∠POC=$\frac{1}{2}$β,
∴tan$\frac{1}{2}$β=$\frac{BC}{AC}$,
∵tanα=$\frac{BD}{BC}$,
∴tanα•tan$\frac{β}{2}$=$\frac{BD}{BC}$•$\frac{BC}{AC}$=$\frac{BD}{AC}$=$\frac{1}{3}$.
故答案为:$\frac{1}{3}$.
点评 此题考查了圆周角定理、相似三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
5. 明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )
明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )
 明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )
明明家今年1~5月份的用电量情况如图所示,则相邻两个月用电量变化最大的是( )| A. | 1月至2月 | B. | 2月至3月 | C. | 3月至4月 | D. | 4月至5月 |
15.二次函数y=$\frac{1}{2}$x2-2的最小值是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
2.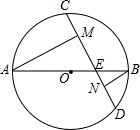 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
 如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )
如图,AB是⊙O的直径,弦CD与AB相交于点E,AM⊥CD,BN⊥CD,垂足分别为M、N.已知CD=5,MN=$\frac{7}{3}$,则线段DN的长为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | 1 | D. | $\sqrt{2}$ |
19.为促进义务教育办学条件均衡,某市投入260万元资金为部分学校添置实验仪器,260万用科学记数法表示为( )
| A. | 260×103 | B. | 26×105 | C. | 2.6×105 | D. | 2.6×106 |
 已知:如图,∠AOB=150°,OC平分∠AOB,∠AOD=90°,则∠COD的度数为15°.
已知:如图,∠AOB=150°,OC平分∠AOB,∠AOD=90°,则∠COD的度数为15°.