Question

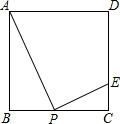已知ABCD是正方形，E是CD上一点，且

CE

DE

=

1

3

，P是BC上的点，若△ABP与△PCE相似，则这样的P有

 

个．

Answer 1

考点：相似三角形的判定

专题：常规题型

分析：设正方形ABCD的边长为4，BP=x，则CE=1，PC=4-x，根据两组对应边的比相等且夹角对应相等的两个三角形相似得到当

AB

CE

=

BP

CP

时，△ABP∽△ECP，即

4

1

=

x

4-x

；当

AB

PC

=

BP

CE

时，△ABP∽△PCE，即

4

4-x

=

x

1

，然后分别解两个方程求出x的值，于是可判断P点的个数．

解答：解：设正方形ABCD的边长为4，BP=x，则CE=1，PC=4-x，
∵∠ABP=∠PCE=90°，
∴当

AB

CE

=

BP

CP

时，△ABP∽△ECP，即

4

1

=

x

4-x

，即得x=

16

5

；
当

AB

PC

=

BP

CE

时，△ABP∽△PCE，即

4

4-x

=

x

1

，整理得x2-4x+4=0，解得x₁=x₂=2，
∴当BP=

16

5

或2时，△ABP与△PCE相似．
故答案为2．

点评：本题考查了相似三角形的判定：两组对应边的比相等且夹角对应相等的两个三角形相似．也考查了正方形的性质．