题目内容
10.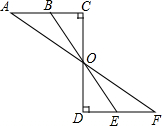 如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:
如图,小强在河的一边,要测河面的一只船B与对岸码头A的距离,他的做法如下:①在岸边确定一点C,使C与A,B在同一直线上;
②在AC的垂直方向画线段CD,取其中点O;
③画DF⊥CD使F、O、A在同一直线上;
④在线段DF上找一点E,使E与O、B共线.
他说测出线段EF的长就是船B与码头A的距离.他这样做有道理吗?为什么?
分析 首先证明△ACO≌△FDO,根据全等三角形的性质可得AO=FO,∠A=∠F,再证明△ABO≌△FEO,进而可得EF=AB.
解答 解:有道理,
∵DF⊥CD,AC⊥CD,
∴∠C=∠D=90°,
∵O为CD中点,
∴CO=DO,
在△ACO和△FDO中$\left\{\begin{array}{l}{∠C=∠D}\\{CO=DO}\\{∠AOC=∠DOF}\end{array}\right.$,
∴△ACO≌△FDO(ASA),
∴AO=FO,∠A=∠F,
在△ABO和△EOF中$\left\{\begin{array}{l}{∠A=∠F}\\{AO=FO}\\{∠AOB=∠FOE}\end{array}\right.$,
∴△ABO≌△FEO(ASA),
∴EF=AB.
点评 此题主要全等三角形的应用,关键是掌握全等三角形的判定方法和性质定理.

练习册系列答案
相关题目
1. 把全体自然数按下面的方式进行排列:按照这样的规律推断,从2014到2016,箭头的方向应是( )
把全体自然数按下面的方式进行排列:按照这样的规律推断,从2014到2016,箭头的方向应是( )
 把全体自然数按下面的方式进行排列:按照这样的规律推断,从2014到2016,箭头的方向应是( )
把全体自然数按下面的方式进行排列:按照这样的规律推断,从2014到2016,箭头的方向应是( )| A. | ↓→ | B. | →↑ | C. | ↑→ | D. | →↓ |
15.已知一个等腰三角形两边长分别为5,6,那么它的周长为( )
| A. | 16 | B. | 17 | C. | 16或17 | D. | 10或12 |
 大学生小王积极相应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电,通过试营销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间满足等式y=ax+b,其中a、b为常数.
大学生小王积极相应“自主创业”的号召,准备投资销售一种进价为每件40元的小家电,通过试营销发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间满足等式y=ax+b,其中a、b为常数.