题目内容
 如图,把等边三角形ABC沿着高AD分成两个全等的直角三角形ABD、ACD,将△ACD绕点D逆时针旋转15°得到△A′C′D,A′D交AB于点E,则
如图,把等边三角形ABC沿着高AD分成两个全等的直角三角形ABD、ACD,将△ACD绕点D逆时针旋转15°得到△A′C′D,A′D交AB于点E,则| AD |
| DE |
考点:旋转的性质
专题:
分析:作DH⊥AB于H,根据等边三角形的性质得∠ABC=∠BAC=60°,而AD为等边三角形ABC的高,则∠BAD=30°,∠ADB=90°,根据含30度的直角三角形三边的关系得AD=
BD,再根据旋转的性质得∠A′DA=15°,则利用三角形外角性质得∠BED=∠EAD+∠ADE=45°,在Rt△BDH中,设BH=x,易得BD=2x,DH=
x,在Rt△EDH中,DE=
DH=
x,所以AD=2
x,然后计算AD和DE的比值.
| 3 |
| 3 |
| 2 |
| 6 |
| 3 |
解答: 解:作DH⊥AB于H,如图,
解:作DH⊥AB于H,如图,
∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
∵AD为等边三角形ABC的高,
∴∠BAD=30°,∠ADB=90°,
∴AD=
BD,
∵△ACD绕点D逆时针旋转15°得到△A′C′D,
∴∠A′DA=15°,
∴∠BED=∠EAD+∠ADE=30°+15°=45°,
在Rt△BDH中,设BH=x,则BD=2x,DH=
x,
在Rt△EDH中,DE=
DH=
x,
∴AD=
•2x=2
x,
∴
=
=
.
故答案为
.
 解:作DH⊥AB于H,如图,
解:作DH⊥AB于H,如图,∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
∵AD为等边三角形ABC的高,
∴∠BAD=30°,∠ADB=90°,
∴AD=
| 3 |
∵△ACD绕点D逆时针旋转15°得到△A′C′D,
∴∠A′DA=15°,
∴∠BED=∠EAD+∠ADE=30°+15°=45°,
在Rt△BDH中,设BH=x,则BD=2x,DH=
| 3 |
在Rt△EDH中,DE=
| 2 |
| 6 |
∴AD=
| 3 |
| 3 |
∴
| AD |
| DE |
2
| ||
|
| 2 |
故答案为
| 2 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质和解直角三角形.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
20140的值是( )
| A、2014 | B、0 |
| C、1 | D、20140 |
 如图,BD是⊙O的切线,AB是⊙O的弦,且OA⊥OD.
如图,BD是⊙O的切线,AB是⊙O的弦,且OA⊥OD.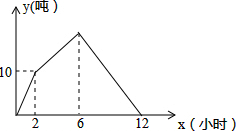 一个生产、装箱流水线,生产前没有积压产品,开始的2小时只生产,2小时后安排装箱(生产没有停止),6小时后生产停止只安排装箱,第12小时时生产流水线上刚好又没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y吨与流水线工作时间x(小时)之间的函数关系如图所示,则流水线上产品装箱的速度为
一个生产、装箱流水线,生产前没有积压产品,开始的2小时只生产,2小时后安排装箱(生产没有停止),6小时后生产停止只安排装箱,第12小时时生产流水线上刚好又没有积压产品,已知流水线的生产、装箱的速度保持不变,流水线上积压产品(没有装箱产品)y吨与流水线工作时间x(小时)之间的函数关系如图所示,则流水线上产品装箱的速度为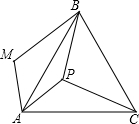 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为