题目内容
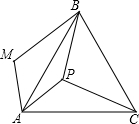 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为考点:旋转的性质,等边三角形的判定与性质,勾股定理的逆定理
专题:计算题
分析:连结MP,根据等边三角形的性质得AB=AC,∠BAC=60°,再根据旋转的性质得AM=AP,∠MAP=∠BAC=60°,BM=CP=10,则可判断△AMP为等边三角形,
所以MP=AP=6,∠APM=60°,在△PBM中通过计算得到PM2+PB2=BM2,根据勾股定理的逆定理得∠BPM=90°,然后利用∠APB=∠APM+BPM进行计算.
所以MP=AP=6,∠APM=60°,在△PBM中通过计算得到PM2+PB2=BM2,根据勾股定理的逆定理得∠BPM=90°,然后利用∠APB=∠APM+BPM进行计算.
解答:解:连结MP,如图,
∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△MAB,
∴AM=AP,∠MAP=∠BAC=60°,BM=CP=10,
∴△AMP为等边三角形,
∴MP=AP=6,∠APM=60°,
在△PBM中,PM=6,BM=10,PB=8,
∵62+82=102,
∴PM2+PB2=BM2,
∴∠BPM=90°,
∴∠APB=∠APM+BPM=60°+90°=150°.
故答案为6,150.

∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△MAB,
∴AM=AP,∠MAP=∠BAC=60°,BM=CP=10,
∴△AMP为等边三角形,
∴MP=AP=6,∠APM=60°,
在△PBM中,PM=6,BM=10,PB=8,
∵62+82=102,
∴PM2+PB2=BM2,
∴∠BPM=90°,
∴∠APB=∠APM+BPM=60°+90°=150°.
故答案为6,150.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的判定与性质和勾股定理的逆定理.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
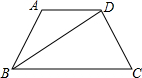 如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4| 3 |
A、4
| ||
| B、12 | ||
C、4
| ||
D、4
|
 一个工人师傅要将一个正方形ABCD(四个角都是直角,四个边都相等)的余料,修剪成如四边形ABEF的零件.其中CE=
一个工人师傅要将一个正方形ABCD(四个角都是直角,四个边都相等)的余料,修剪成如四边形ABEF的零件.其中CE=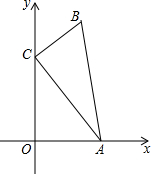 如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为
如图,在△ABC中,∠ACB=90°,AC=8,BC=3,点A、C分别在x轴、y轴上,当点A在x轴上运动时,点C随之在y轴上运动,在运动过程中,点B到原点O的最大距离为 直角三角形在正方形网格纸中的位置如图,则tanα=
直角三角形在正方形网格纸中的位置如图,则tanα= 如图,把等边三角形ABC沿着高AD分成两个全等的直角三角形ABD、ACD,将△ACD绕点D逆时针旋转15°得到△A′C′D,A′D交AB于点E,则
如图,把等边三角形ABC沿着高AD分成两个全等的直角三角形ABD、ACD,将△ACD绕点D逆时针旋转15°得到△A′C′D,A′D交AB于点E,则 一次越野赛跑中,当小明跑了1600米时,小刚跑了1450米.此后两人分别以另一速度匀速跑完全程,两人到达终点时均停止跑步,如图所示 的折线图表示了后一段路程中,两人之间的距离y(单位:米)与后一段路程跑步所用的时间x(秒)之间的关系,则这次越野赛跑的全程为
一次越野赛跑中,当小明跑了1600米时,小刚跑了1450米.此后两人分别以另一速度匀速跑完全程,两人到达终点时均停止跑步,如图所示 的折线图表示了后一段路程中,两人之间的距离y(单位:米)与后一段路程跑步所用的时间x(秒)之间的关系,则这次越野赛跑的全程为