题目内容
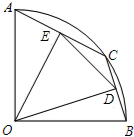 如图,在半径为5的扇形AOB中,∠AOB=90°,点C是
如图,在半径为5的扇形AOB中,∠AOB=90°,点C是 |
| AB |
(1)求线段OD、DE的长;
(2)求线段OE的长.
考点:垂径定理,勾股定理,三角形中位线定理
专题:计算题
分析:(1)连结AB,如图1,根据垂径定理,由OD⊥BC得到BD=
BC=1,再在Rt△OBD中,利用勾股定理可计算出OD=2
,然后证明DE为△ABC的中位线,根据三角形中位线性质得到DE=
AB,接着证明△AOB为等腰直角三角形得到AB=
OB=5
,所以DE=
;
(2)作DH⊥OE,连结OC,如图2先证明∠2+∠3=45°,得到△ODH为等腰直角三角形,则OH=DH=
OD=2
,再在Rt△DHE中,利用勾股定理计算出HE=
,然后由OE=OH+HE计算即可.
| 1 |
| 2 |
| 6 |
| 1 |
| 2 |
| 2 |
| 2 |
5
| ||
| 2 |
(2)作DH⊥OE,连结OC,如图2先证明∠2+∠3=45°,得到△ODH为等腰直角三角形,则OH=DH=
| ||
| 2 |
| 3 |
| ||
| 2 |
解答: 解:(1)连结AB,如图1,
解:(1)连结AB,如图1,
∵OD⊥BC,
∴BD=CD=
BC=1,
在Rt△OBD中,∵BD=1,OB=5,
∴OD=
=2
,
∵OE⊥AC,
∴AE=CE,
∴DE为△ABC的中位线,
∴DE=
AB,
∵∠AOB=90°,
∴△AOB为等腰直角三角形,
∴AB=
OB=5
,
∴DE=
;
即线段OD、DE的长分别为2
,
;
(2)作DH⊥OE,连结OC,如图2,
∵OC=OB,OD垂直平分BC,
∴OD平分∠BOC,即∠3=∠4,
同理可得∠1=∠2,
而∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°,
∴△ODH为等腰直角三角形,
∴OH=DH=
OD=
•2
=2
,
在Rt△DHE中,∵DH=2
,DE=
,
∴HE=
=
,
∴OE=OH+HE=2
+
.
 解:(1)连结AB,如图1,
解:(1)连结AB,如图1,∵OD⊥BC,
∴BD=CD=
| 1 |
| 2 |
在Rt△OBD中,∵BD=1,OB=5,
∴OD=
| OB2-BD2 |
| 6 |
∵OE⊥AC,
∴AE=CE,
∴DE为△ABC的中位线,
∴DE=
| 1 |
| 2 |
∵∠AOB=90°,
∴△AOB为等腰直角三角形,
∴AB=
| 2 |
| 2 |
∴DE=
5
| ||
| 2 |
即线段OD、DE的长分别为2
| 6 |
5
| ||
| 2 |
(2)作DH⊥OE,连结OC,如图2,

∵OC=OB,OD垂直平分BC,
∴OD平分∠BOC,即∠3=∠4,
同理可得∠1=∠2,
而∠1+∠2+∠3+∠4=90°,
∴∠2+∠3=45°,
∴△ODH为等腰直角三角形,
∴OH=DH=
| ||
| 2 |
| ||
| 2 |
| 6 |
| 3 |
在Rt△DHE中,∵DH=2
| 3 |
5
| ||
| 2 |
∴HE=
| DE2-DH2 |
| ||
| 2 |
∴OE=OH+HE=2
| 3 |
| ||
| 2 |
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和三角形中位线定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
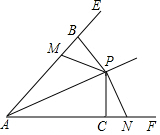 如图所示,已知∠EAF,FB⊥AE于点B,PC⊥AF于点C,M,N分别是射线AE,AF上的点,∠PNC=∠PMB,PM=PN.求证:AP平分∠EAF.
如图所示,已知∠EAF,FB⊥AE于点B,PC⊥AF于点C,M,N分别是射线AE,AF上的点,∠PNC=∠PMB,PM=PN.求证:AP平分∠EAF. 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度.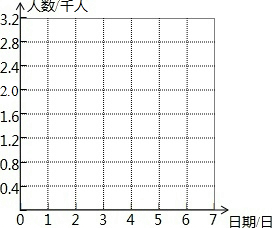 “十一”黄金周期间,某游乐园在7天假期中每天游园的人数变化如下表:
“十一”黄金周期间,某游乐园在7天假期中每天游园的人数变化如下表: 如图所示,在△ABC中,BC=12cm,BC边上的高AN=6cm,四边形DHFE是矩形.如果设DE=x,四边形DHFE的面积是y,则y与x之间的关系式是什么?当x等于何值时,y值最大面积?
如图所示,在△ABC中,BC=12cm,BC边上的高AN=6cm,四边形DHFE是矩形.如果设DE=x,四边形DHFE的面积是y,则y与x之间的关系式是什么?当x等于何值时,y值最大面积? 如图,直线AB、CD相交于点O,∠1=35°,∠2=75°,求∠EOB的度数.
如图,直线AB、CD相交于点O,∠1=35°,∠2=75°,求∠EOB的度数. 已知,AB=AD,CB=CD.
已知,AB=AD,CB=CD.