题目内容

如图所示，在△ABC中，BC=12cm，BC边上的高AN=6cm，四边形DHFE是矩形．如果设DE=x，四边形DHFE的面积是y，则y与x之间的关系式是什么？当x等于何值时，y值最大面积？
考点：二次函数的应用
专题：
分析：根据相似三角形的判定与性质得出△ADE∽△ABC，则
AM
AN
=
DE
BC
，进而表示出AM的长，即可表示出四边形DHFE的面积，求出最值即可．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∴
AM
AN
=
DE
BC
，
∴AM=
AN×DE
BC
=
6x
12
=
x
2
，
故MN=DH=（6-
x
2
）cm，
∴y=DE×DH=x（6-
x
2
）=-
1
2
x2+3x=-
1
2
（x-3）2+4.5．
故当x=3时，y值最大面积为4.5cm2．
点评：此题主要考查了二次函数的应用以及相似三角形的判定与性质，表示出MN的长是解题关键．
练习册系列答案
相关题目
某批发商店经销一种高档水果，如果每千克成本15元，售价25元，每天可售出500kg，经市场调查发现，在进货价不变的情况下，若每千克涨价5元，日销量将减少100kg，现该商店要保证每天盈利6000元，同时又要使顾客得到实惠，那么每千克应定价多少元？
先阅读材料，再完成下面的问题：
方程x+
1
x
=2+
1
2
的解是x1=2，x2=
1
2
；x+
1
x
=3+
1
3
的解是x1=3，x2=
1
3
．
（1）观察上述方程的解，试猜想关于x的方程x+
1
x
=c+
1
c
的解是
 
．
（2）把关于x的方程x+
1
x-1
=a+
1
a-1
变形为方程x+
1
x
=c+
1
c
的形式是
 
，方程的解是
 
，解决这个问题的数学思想是
 
x．
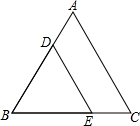如图，△ABC和△DBE均为等边三角形，已知AB=6，BD=2
3
，现把△DBE绕点B逆时针旋转，所得三角形记为△D′BE′，连接AE′，当∠AE′D′=60°时，点A到直线D′B的距离等于
 
．
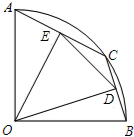如图，在半径为5的扇形AOB中，∠AOB=90°，点C是
AB
上的一点，且BC=2，OD⊥BC，OE⊥AC，垂足分别为D、E．
（1）求线段OD、DE的长；
（2）求线段OE的长．
如图，在△PMN中，点E在PN上，点F在MN上，在PM上找一点Q，使△EFQ的周长最小，并说明理由．
因式分解：x2-4+12y-9y2．
如图，PA，PB是半径为2的⊙O的两条切线，点A，B分别为切点，∠APB=60°，连接OP与弦AB相交于点C，与⊙O交于点D．
（1）求弦AB的长；
（2）求出阴影部分的面积；（结果保留π）
（3）连接DB，求证：S△PBD=2S△BOC．
我们知道：点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．所以式子|x-3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离．
根据上述材料，直接下列问题答案：
（1）|5-（-2）|的值为
 
；  
（2）若|x-3|=1，则x的值为
 
；
（3）若|x-3|=|x+1|，则x的值为
 
； 
（4）若|x-3|+|x+1|=7，则x的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网