题目内容
19.解下列方程:(1)2(x+3)2=x(x+3);
(2)x2-2$\sqrt{5}$x+2=0;
(3)(x+1)2-3(x+1)+2=0.
分析 (1)直接利用提取公因式法分解因式进而解方程得出答案;
(2)直接利用公式法解方程得出答案;
(3)直接利用十字相乘法分解因式进而解方程得出答案.
解答 解:(1)2(x+3)2=x(x+3)
(x+3)[2(x+3)-x]=0,
则(x+3)(x+6)=0,
解得:x1=-3,x2=-6;
(2)x2-2$\sqrt{5}$x+2=0
b2-4ac=(2$\sqrt{5}$)2-4×1×2=12>0,
则x=$\frac{2\sqrt{5}±2\sqrt{3}}{2}$,
故x1=$\sqrt{5}$+$\sqrt{3}$,x2=$\sqrt{5}$-$\sqrt{3}$;
(3)(x+1)2-3(x+1)+2=0
(x+1-2)(x+2-1)=0,
解得:x1=1,x2=-1.
点评 此题主要考查了公式法以及因式分解法解方程,正确运用因式分解法解方程是解题关键.

练习册系列答案
相关题目
9. 如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )
如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )
 如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )
如图,在点M,N,P,Q中,一次函数y=kx+2(k<0)的图象不可能经过的点是( )| A. | M | B. | N | C. | P | D. | Q |
10.一个多边形的每一个外角都是45°,那么这个多边形是( )
| A. | 八边形 | B. | 九边形 | C. | 十边形 | D. | 十二边形 |
7. 如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在AD的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠C=∠CDE | D. | ∠C+∠CDA=180° |
14.下列各式中,是最简二次根式的是( )
| A. | $\sqrt{{m}^{2}+1}$ | B. | $\sqrt{\frac{a}{5}}$ | C. | $\sqrt{27}$ | D. | $\sqrt{5{a}^{2}b}$ |
4.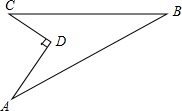 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
 如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )
如图所示,有一块地ABCD,已知AD=4米,CD=3米,∠ADC=90°,AB=13米,BC=12米,则这块地的面积为( )| A. | 60米2 | B. | 48米2 | C. | 30米2 | D. | 24米2 |
2.某班在一次数学测试后,成绩统计如表:该班这次数学测试的平均成绩是82.
| 分数 | 100 | 90 | 80 | 70 | 60 | 50 |
| 人数 | 7 | 14 | 17 | 8 | 2 | 2 |
3.统计学校20名女子合唱团成员的身高,统计结果如下表.
根据表中信息可以判断该排球队员的平均身高为( )
| 身高(cm) | 163 | 164 | 165 | 166 | 167 |
| 人数(个) | 1 | 1 | 3 | 7 | 8 |
| A. | 164cm | B. | 165cm | C. | 166cm | D. | 157cm |