题目内容
11.当a=-3时,分式$\frac{a+3}{3-a}$的值为0.分析 分式值为零的条件是分子等于零且分母不等于零.
解答 解:∵分式$\frac{a+3}{3-a}$的值为0,
∴a+3=0且3-a≠0,
解得:a=-3.
故答案为:-3.
点评 本题主要考查的是分式值为零的条件,熟练掌握分式值为零的条件是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 鸡兔同笼问题是我国古代著名趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?经计算可得( )
鸡兔同笼问题是我国古代著名趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?经计算可得( )
 鸡兔同笼问题是我国古代著名趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?经计算可得( )
鸡兔同笼问题是我国古代著名趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头;从下面数,有94只脚.求笼中各有几只鸡和兔?经计算可得( )| A. | 鸡23只,兔12只 | B. | 鸡12只,兔23只 | C. | 鸡15只,兔20只 | D. | 鸡20只,兔15只 |
2.如果x2+mx+16是完全平方式,则常数m的值是( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 17 |
6.已知一元二次方程2x2+mx-7=0的一个根为x=1,则m的值与方程的另一根分别是( )
| A. | 5,1 | B. | -5,2 | C. | 5,-$\frac{7}{2}$ | D. | -5,-$\frac{7}{2}$ |
15.某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用-支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
(1)在这个变化过程中,每月的乘车人数x是自变量,每月的利润y是因变量;
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
| x(人) | 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
| y(元) | -3000 | -2000 | -1000 | 0 | 1000 | 2000 | … |
(2)观察表中数据可知,每月乘客量达到观察表中数据可知,每月乘客量达到2000人以上时,该公交车才不会亏损;
(3)请你估计当每月乘车人数为3500人时,每月利润为多少元?
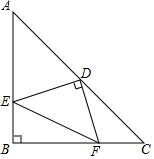 如图,在Rt△ABC中,AB=BC,∠B=90°,D是AC的中点,E、F分别是AB、BC上的点,且DE⊥DF,若AE=12,CF=5,求AC、EF的长.
如图,在Rt△ABC中,AB=BC,∠B=90°,D是AC的中点,E、F分别是AB、BC上的点,且DE⊥DF,若AE=12,CF=5,求AC、EF的长.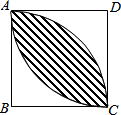 已知正方形ABCD的边长为1,分别以B,D为圆心,以1为半径画弧,如图所示,则阴影部分的面积为$\frac{π}{2}$-1.
已知正方形ABCD的边长为1,分别以B,D为圆心,以1为半径画弧,如图所示,则阴影部分的面积为$\frac{π}{2}$-1.