题目内容
9.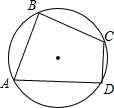 如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
分析 过点B作BE⊥AD于点E,过点C作CF⊥BE于点F,根据AB=2,∠A=60°可求出BE的长及∠CNF的度数,再由圆内接四边形的性质得出∠D=90°,由此可得出四边形CDEF是矩形,进而可得出EF的长,由BF=BE-EF可得出BF的长,根据锐角三角函数的定义可得出BC的长.
解答 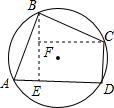 解:过点B作BE⊥AD于点E,过点C作CF⊥BE于点F,
解:过点B作BE⊥AD于点E,过点C作CF⊥BE于点F,
∵AB=2,∠A=60°,
∴∠ABE=30°,BE=AB•sin60°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∵∠B=90°,
∴∠CBE=∠B-∠ABE=90°-30°=60°.
∵四边形ABCD是圆内接四边形,∠B=90°,
∴∠D=180°-90°=90°,
∴四边形CDEF是矩形,
∴EF=CD=1,
∴BF=BE-1=$\sqrt{3}$-1.
∵∠CBE=60°,
∴BC=$\frac{BF}{cos60°}$=$\frac{\sqrt{3}-1}{\frac{1}{2}}$=2$\sqrt{3}$-2.
点评 本题考查的是圆内接四边形的性质,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.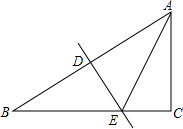 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
 如图,数轴上的点A,B表示的数分别是a-b,a+b.
如图,数轴上的点A,B表示的数分别是a-b,a+b.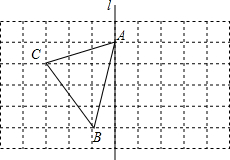 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上. 如图,已知直线AB∥DF,∠D+∠B=180°,
如图,已知直线AB∥DF,∠D+∠B=180°,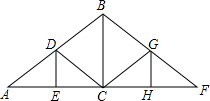 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DC垂直于横梁AC,AB=8m,∠A=30°,立柱BC,DE要多长?
如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DC垂直于横梁AC,AB=8m,∠A=30°,立柱BC,DE要多长?