题目内容
20.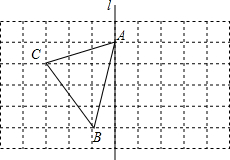 如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.
如图,在长度为1个单位长度的小正方形组成的长方形中,点A,B,C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为$\frac{11}{2}$;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为5.
分析 (1)根据轴对称的性质画出△ABC关于直线l成轴对称的△AB′C′即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可;
(3)连接BC′交直线l于点P,则P点即为所求点,PB+PC的最短长度为线段BC′的长.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)S△ABC=4×3-$\frac{1}{2}$×1×3-$\frac{1}{2}$×2×3-$\frac{1}{2}$×1×4
=12-$\frac{3}{2}$-3-2
=$\frac{11}{2}$.
故答案为:$\frac{11}{2}$;
(3)连接BC′交直线l于点P,则P点即为所求点,此时PB+PC的最短长度为线段BC′的长,BC′=$\sqrt{{3}^{2}+{4}^{2}}$=5.
故答案为:5.
点评 本题考查的是作图-轴对称变换,熟知轴对称图形的作法是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.已知等腰三角形中,一个角为80°,则该等腰三角形的底角度数是( )
| A. | 80° | B. | 50° | C. | 80°或50° | D. | 20° |
8. 问题背景
问题背景
若矩形的周长为1,则可求出该矩形面积的最大值,我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:s=-x2+$\frac{1}{2}x(x>0)$,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为:y=2(x+$\frac{1}{x}$)(x>0),问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值.
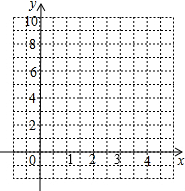
(1)实践操作:填写下表,并用描点法画出函数y=2(x+$\frac{1}{x}$)(x>0)的图象:
(2)观察猜想:观察该函数的图象,猜想当x=1时,函数y=2(x+$\frac{1}{x}$)(x>0)有最小值(填“大”或“小”),是4.
(3)推理论证:问题背景中提到,通过配方可求二次函数s=-x2+$\frac{1}{2}$x(x>0)的最大值,请你尝试通过配方求函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,x=($\sqrt{x}$)2).
 问题背景
问题背景若矩形的周长为1,则可求出该矩形面积的最大值,我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:s=-x2+$\frac{1}{2}x(x>0)$,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为:y=2(x+$\frac{1}{x}$)(x>0),问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数y=2(x+$\frac{1}{x}$)(x>0)的图象:
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … |
(3)推理论证:问题背景中提到,通过配方可求二次函数s=-x2+$\frac{1}{2}$x(x>0)的最大值,请你尝试通过配方求函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,x=($\sqrt{x}$)2).
5.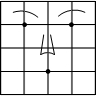 如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )
如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )
 如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )
如图是小强画出的一张脸的简笔画,他对小刚说:“我用(0,2)表示左眼的位置,用(2,2)表示右眼的位置,”那么嘴的位置可表示成( )| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (1,-1) |
10.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2014次变换后所得A点坐标是( )
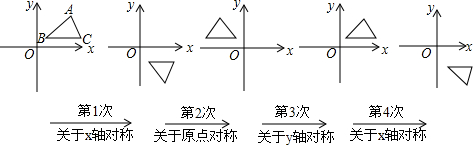

| A. | (a,-b) | B. | (-a,-b) | C. | (-a,b) | D. | (a,b) |
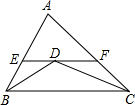 如图,△ABC中,AB=5,AC=8,BD,CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )
如图,△ABC中,AB=5,AC=8,BD,CD分别平分∠ABC,∠ACB,过点D作直线平行于BC,交AB,AC于E,F,则△AEF的周长为( )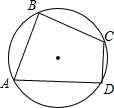 如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.