题目内容
19. 如图,数轴上的点A,B表示的数分别是a-b,a+b.
如图,数轴上的点A,B表示的数分别是a-b,a+b.(1)求A,B两点间的距离;
(2)根据图中信息,写出一个正确的结论或提出一个合理的问题(不需解答)
分析 (1)A,B两点间的距离等于A,B表示的数的差的绝对值;
(2)轴上两数的位置关系可比较两数的大小.
解答 解:(1)AB=(a+b)-(a-b)=a+b-a+b=2b;
(2)根据图形可知:a-b<0,a+b>0.
点评 本题主要考查的是数轴的认识,掌握数轴的相关概念是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
7.下表是某服装店的原价表,国庆期间该店优惠大酬宾,外套按原价打六折出售,衬衫和裤子按原价打八折出售,已知这三种服饰共卖出200件,共得33860元.设外套卖出x件,由题意可得方程( )
| 服饰 | 原价(元) |
| 外套 | 299 |
| 衬衫 | 199 |
| 裤子 | 199 |
| A. | 0.8×199x+0.6×299(200+x)=33860 | B. | 0.8×199x+0.6×299(200-x)=33860 | ||
| C. | 0.6×299x+0.8×199(200+x)=33860 | D. | 0.6×299x+08×199(200-x)=33860 |
4.“$\frac{36}{25}$的平方根是±$\frac{6}{5}$”用数学式表示为( )
| A. | $\sqrt{\frac{36}{25}}$=$±\frac{6}{5}$ | B. | $±\sqrt{\frac{36}{25}}$=$±\frac{6}{5}$ | C. | $\sqrt{\frac{36}{25}}$=$\frac{6}{5}$ | D. | -$\sqrt{\frac{36}{25}}$=-$\frac{6}{5}$ |
11.已知等腰三角形中,一个角为80°,则该等腰三角形的底角度数是( )
| A. | 80° | B. | 50° | C. | 80°或50° | D. | 20° |
8. 问题背景
问题背景
若矩形的周长为1,则可求出该矩形面积的最大值,我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:s=-x2+$\frac{1}{2}x(x>0)$,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为:y=2(x+$\frac{1}{x}$)(x>0),问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值.
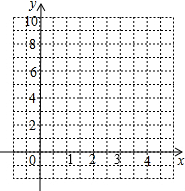
(1)实践操作:填写下表,并用描点法画出函数y=2(x+$\frac{1}{x}$)(x>0)的图象:
(2)观察猜想:观察该函数的图象,猜想当x=1时,函数y=2(x+$\frac{1}{x}$)(x>0)有最小值(填“大”或“小”),是4.
(3)推理论证:问题背景中提到,通过配方可求二次函数s=-x2+$\frac{1}{2}$x(x>0)的最大值,请你尝试通过配方求函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,x=($\sqrt{x}$)2).
 问题背景
问题背景若矩形的周长为1,则可求出该矩形面积的最大值,我们可以设矩形的一边长为x,面积为s,则s与x的函数关系式为:s=-x2+$\frac{1}{2}x(x>0)$,利用函数的图象或通过配方均可求得该函数的最大值.
提出新问题
若矩形的面积为1,则该矩形的周长有无最大值或最小值?若有,最大(小)值是多少?
分析问题
若设该矩形的一边长为x,周长为y,则y与x的函数关系式为:y=2(x+$\frac{1}{x}$)(x>0),问题就转化为研究该函数的最大(小)值了.
解决问题
借鉴我们已有的研究函数的经验,探索函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数y=2(x+$\frac{1}{x}$)(x>0)的图象:
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … |
(3)推理论证:问题背景中提到,通过配方可求二次函数s=-x2+$\frac{1}{2}$x(x>0)的最大值,请你尝试通过配方求函数y=2(x+$\frac{1}{x}$)(x>0)的最大(小)值,以证明你的猜想.〔提示:当x>0时,x=($\sqrt{x}$)2).
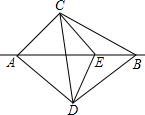 如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.
如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.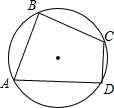 如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.