题目内容
1.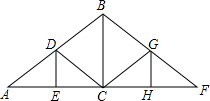 如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DC垂直于横梁AC,AB=8m,∠A=30°,立柱BC,DE要多长?
如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC,DC垂直于横梁AC,AB=8m,∠A=30°,立柱BC,DE要多长?
分析 由DE⊥AC,BC⊥AC,AB=8m,∠A=30°,易求BC,DE=$\frac{1}{2}$AD,由D是斜梁AB的中点,求得AD,进而可求DE.
解答 解:∵DE⊥AC,BC⊥AC,AB=8m,∠A=30°,
∴BC=$\frac{1}{2}$AB=4(m),DE=$\frac{1}{2}$AD,
∵D是斜梁AB的中点,
∴AD=$\frac{1}{2}$AB=4(m),
∴DE=$\frac{1}{2}$AD=2(m).
答:立柱BC的长4m,DE的长2m.
点评 此题考查含30°直角三角形的性质:在直角三角形中,30°的角所对的直角边是斜边的一半.

练习册系列答案
相关题目
11.已知等腰三角形中,一个角为80°,则该等腰三角形的底角度数是( )
| A. | 80° | B. | 50° | C. | 80°或50° | D. | 20° |
13.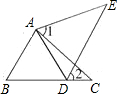 如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是( )
如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是( )
 如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是( )
如图,∠1=∠2,要证明△ABC≌△ADE,还需补充的条件是( )| A. | AB=AD,AC=AE | B. | AB=AD,BC=DE | C. | AB=DE,BC=AE | D. | AC=AE,BC=DE |
10.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2014次变换后所得A点坐标是( )
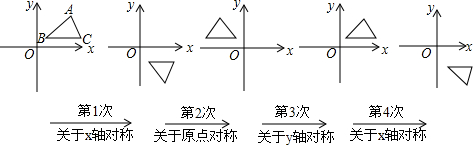

| A. | (a,-b) | B. | (-a,-b) | C. | (-a,b) | D. | (a,b) |
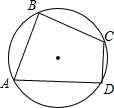 如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
如图,点A、B、C、D在⊙O上,∠A=60°,∠B=90°,AB=2,CD=1,求BC的长.
 如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长为20cm,AE=5cm,则△ABC的周长是30cm.
如图,在△ABC中,AC的垂直平分线交AC于E,交BC于D,△ABD的周长为20cm,AE=5cm,则△ABC的周长是30cm.