题目内容
 如图,⊙O是△ABC的外接圆,若AC=12,sinB=
如图,⊙O是△ABC的外接圆,若AC=12,sinB=| 4 |
| 5 |
| A、6.5 | B、7.5 |
| C、8.5 | D、10 |
考点:垂径定理,圆周角定理,解直角三角形
专题:计算题
分析:作直径AD,连结DC,根据圆周角定理得∠D=∠B,则sinD=sinB=
,再根据圆周角定理由AD为直径得∠ACD=90°,在Rt△ADC中,利用正弦的定义可计算出AD=15,则OA=
AD=7.5.
| 4 |
| 5 |
| 1 |
| 2 |
解答:解: 作直径AD,连结DC,如图,
作直径AD,连结DC,如图,
∵∠D=∠B,
∴sinD=sinB=
,
∵AD为直径,
∴∠ACD=90°,
在Rt△ADC中,sinD=
,
∴AD=
=15,
∴OA=
AD=7.5,
即⊙O的半径为7.5.
故选B.
 作直径AD,连结DC,如图,
作直径AD,连结DC,如图,∵∠D=∠B,
∴sinD=sinB=
| 4 |
| 5 |
∵AD为直径,
∴∠ACD=90°,
在Rt△ADC中,sinD=
| AC |
| AD |
∴AD=
| 12 | ||
|
∴OA=
| 1 |
| 2 |
即⊙O的半径为7.5.
故选B.
点评:本题考查了垂径定理:平分弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了圆周角定理和锐角三角函数的定义.

练习册系列答案
相关题目
已知点P(2-a,3a+6)在第四象限,且到两坐标轴的距离相等,则P点的坐标为( )
| A、(2,-2) |
| B、(3,-3) |
| C、(4,-4) |
| D、(6,-6) |
已知下列命题,其中真命题的个数是( )
①若a2=b2,则a=b;
②对角线互相垂直平分的四边形是菱形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数y=
中,如果函数值y<1时,那么自变量x>2.
①若a2=b2,则a=b;
②对角线互相垂直平分的四边形是菱形;
③两组对角分别相等的四边形是平行四边形;
④在反比例函数y=
| 2 |
| x |
| A、4个 | B、3个 | C、2个 | D、1个 |
若二次根式
在实数范围内有意义,则x的取值范围是( )
| 6-3x |
| A、x≤2 | B、x≥2 |
| C、x<2 | D、x≠2 |
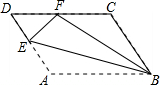 如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处,若△FDE的周长为6,△FCB的周长为20,那么CF的长为
如图,平行四边形ABCD中,点E在AD上,以BE为折痕,把△ABE向上翻折,点A正好落在CD边的点F处,若△FDE的周长为6,△FCB的周长为20,那么CF的长为 水仙花是漳州市花,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为
水仙花是漳州市花,如图,在长为14m,宽为10m的长方形展厅,划出三个形状、大小完全一样的小长方形摆放水仙花,则每个小长方形的周长为