题目内容
证明：当n为大于2的整数时，n5-5n3+4n能被120整除．
考点：因式分解的应用
专题：
分析：把所给的等式利用因式分解写成乘积的形式：n5-5n3+4n=（n-2）（n-1）n（n+1）（n+2）．因为n-2、n-1、n、n+1、n+2是连续的五个正整数，所以其中必有一个是2的倍数、一个是3的倍数，一个是4的倍数、一个是5的倍数，可知n5-5n3+4n=（n-2）（n-1）n（n+1）（n+2）一定是120的倍数，所以最大约数为120．
解答：证明：∵n5-5n3+4n=（n-2）（n-1）n（n+1）（n+2）．
∴对一切大于2的正整数n，数n5-5n3+4n都含有公约数1×2×3×4×5=120，
∴当n为大于2的整数时，n5-5n3+4n能被120整除．
∴对一切大于2的正整数n，数n5-5n3+4n都含有公约数1×2×3×4×5=120，
∴当n为大于2的整数时，n5-5n3+4n能被120整除．
点评：主要考查了利用因式分解的方法解决实际问题．要先分解因式并根据其实际意义来求解．
练习册系列答案
相关题目
如图，⊙O是△ABC的外接圆，若AC=12，sinB=| 4 |
| 5 |
| A、6.5 | B、7.5 |
| C、8.5 | D、10 |
式子2014-a2+2ab-b2的最大值是（ ）
| A、2012 | B、2013 |
| C、2014 | D、2015 |
如图，在四边形ABCD中，∠ACB=90°，AC=BC．过点B作BE∥AD，交CD于点E，在CD上截取DF=CE，如果∠1=∠2．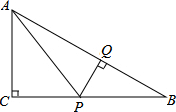
在Rt△ABC中，∠C=90°，P是BC边上不同于B、C的一动点，过P作PQ⊥AB，垂足为Q，连接AP．
