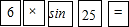��Ŀ����
4���ڵȱ�������ABC�У���E��ֱ��AB�ϣ���D������CB�ϣ���CE=DE��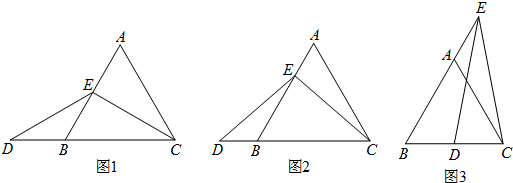
��1�����������̽������
��ͼ1������E��AB�е�ʱ��ȷ���߶�AE��BD�Ĵ�С��ϵ������ֱ��д�����ۣ�AE=BD�����������������=������
��2����������������̽��
��ͼ2������E���߶�AB�ϳ��˵���е������һ��ʱ����ʱ����1���еĽ����Ƿ����仯��д����IJ��벢����֤����
��3����չ����
��ͼ3������E��BA���ӳ�����ʱ����D��BC���ϣ���CE=DE����1���еĽ����Ƿ����仯��д����IJ��벢����֤����
���� ��1�����ݵȱ������ε����ʵõ���BCE=30�㣬AE=BE�����ݵ��������ε����ʵõ���D=��ECD=30�㣬���������ε���ǵ����ʵõ���DEB=30�㼴�ɵõ����ۣ�
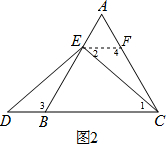
��2����ͼ2����E��EF��BC��AC��F�����ݵȱ������ε����ʵõ���ABC=��ACB=60�㣬����ƽ���ߵ����ʵõ���AEF=��AFE=60���Ƴ���AEF�ǵȱ������Σ�����ȫ�������ε����ʵõ�BD=FE�����������õ����ۣ�
��3����E��EF��BC��CA���ӳ�����F�����ǵõ���1=��F�����ݵȱ������ε����ʵõ���EAF=��2=��F=60�㣬����ȫ�������ε����ʵõ�BD=EF�����������õ����ۣ�
���  �⣺��1���ߡ�ABC�ǵȱ������Σ���E��AB�е㣬
�⣺��1���ߡ�ABC�ǵȱ������Σ���E��AB�е㣬
���BCE=30�㣬AE=BE��
��DE=CE��
���D=��ECD=30�㣬
�ߡ�ABC=60�㣬
���DEB=30�㣬
���D=��DEB��
��BD=BE��
��AE=BD��
��2����1���еĽ��۲������仯��
���ɣ���ͼ2����E��EF��BC��AC��F��
�ߡ�ABC�ǵȱ������Σ�
���ABC=��ACB=60�㣬
���AEF=��AFE=60�㣬��3=120�㣬
���AEF�ǵȱ������Σ�
��AE=EF����4=120�㣬
���3=��4��
��DE=CE��
���D=��1��
���D=��2��
�ڡ�BDE���FEC�У�$\left\{\begin{array}{l}{��D=��2}\\{��3=��4}\\{DE=CE}\end{array}\right.$��
���BDE�ա�FEC��
��BD=FE��
��AE=BD��
��3���������仯��
���ɣ���E��EF��BC��CA���ӳ�����F��
���1=��F����BCE+��CEF=180�㣬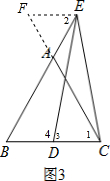
�ߡ�B=��1=��BAC=60�㣬
���EAF=��2=��F=60�㣬
��AE=EF����F=��B��
��DE=CE��
���3=��BCE��
�ߡ�3+��4=180�㣬
���4=��CEF��
�ڡ�BDE���FEC�У�$\left\{\begin{array}{l}{��4=��CEF}\\{��B=��F}\\{DE=CE}\end{array}\right.$��
���BDE�ա�FEC��
��BD=EF��
��AE=BD��
���� ���⿼����ȫ�������ε��ж������ʣ��ȱ������ε����ʣ����������ε����ʣ�ƽ���ߵ����ʣ���ȷ�����������߹���ȱ��������ǽ���Ĺؼ���

| A�� | 3.5��108 | B�� | 35��108 | C�� | 35��10-8 | D�� | 3.5��10-8 |
| A�� | 2 | B�� | -2 | C�� | 2��-2 | D�� | 2��-1 |
| A�� | 2.16 | B�� | 2.15 | C�� | 2.14 | D�� | 2.13 |
| A�� | m��0 | B�� | m��1 | C�� | m��0 | D�� | m��1 |
| A�� | x��-$\frac{1}{3}$ | B�� | x��$\frac{1}{3}$ | C�� | x��$\frac{1}{3}$ | D�� | x��-$\frac{1}{3}$ |
 ��ͼ��һ�������ݶ����ּܵĿ��AC=12m������AB=BC����BAC=25�㣮���ÿ�ѧ������������AB�ij��������а���˳����ȷ���ǣ�������
��ͼ��һ�������ݶ����ּܵĿ��AC=12m������AB=BC����BAC=25�㣮���ÿ�ѧ������������AB�ij��������а���˳����ȷ���ǣ�������