题目内容
19.在反比例函数y=$\frac{1-k}{x}$的图象的任一支上,y都随x的增大而增大,则k的值可以是( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 根据反比例函数的单调性结合反比例函数的性质可得出关于k的一元一次不等式,解不等式即可得出k的取值范围,再结合四个选项即可得出结论.
解答 解:∵在反比例函数y=$\frac{1-k}{x}$的图象的任一支上,y都随x的增大而增大,
∴1-k<0,
解得:k>1.
故选D.
点评 本题考查了反比例函数的性质以及解一元一次不等式,解题的关键是得出1-k<0.本题属于基础题,难度不大,解决该题型题目时,根据反比例函数的单调性结合反比例函数的性质找出关于k的不等式是关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
9.下列整式乘法的运算中,正确的是( )
| A. | (a+b)(a-b)=a2-b2 | B. | (a+b)2=a2+b2 | C. | (a+b)(a-b)=2a-2b | D. | (a-b)2=a2-2ab-b2 |
10.反比例函数y=-$\frac{3}{x}$的图象上有(-2,y1);(-3,y2)两点,则y1与y2的大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不确定 |
7.以下四个命题中真命题是( )
①三角形有且只有一个内切圆;
②四边形的内角和与外角和相等;
③顺次连接四边形各边中点所得的四边形一定是菱形;
④一组对边平行且一组对角相等的四边形是平行四边形.
①三角形有且只有一个内切圆;
②四边形的内角和与外角和相等;
③顺次连接四边形各边中点所得的四边形一定是菱形;
④一组对边平行且一组对角相等的四边形是平行四边形.
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ②③④ |
11.小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为80分、85分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )
| A. | 255分 | B. | 84.5分 | C. | 85.5分 | D. | 86.5分 |
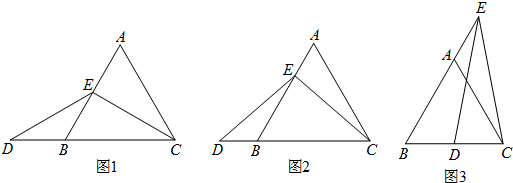
 如图,在?ABCD中,AE⊥BC,垂足为E,AB=5,BC=8,sinB=$\frac{4}{5}$,那么S△CDE=10.
如图,在?ABCD中,AE⊥BC,垂足为E,AB=5,BC=8,sinB=$\frac{4}{5}$,那么S△CDE=10.