题目内容
3. 如图,在△ABC中,AB=AC,点M在BC边上,ME⊥AB于点E,MF⊥AC于点F,且ME=MF.求证:MB=MC.
如图,在△ABC中,AB=AC,点M在BC边上,ME⊥AB于点E,MF⊥AC于点F,且ME=MF.求证:MB=MC.
分析 根据等边对等角的性质可得∠B=∠C,然后根据“角角边”证明△BME和△CMF全等,再根据全等三角形对应边相等即可得证.
解答 证明:∵AB=AC,
∴∠B=∠C,
∵ME⊥AB,MF⊥AC,
∴∠BEM=∠CFM=90°,
在△BME和△CMF中,
∵$\left\{\begin{array}{l}{∠B=∠C}\\{∠BEM=∠CFM=90°}\\{ME=MF}\end{array}\right.$,
∴△BME≌△CMF(AAS),
∴MB=MC.
点评 本题考查了全等三角形的判定与性质,等腰三角形两底角相等的性质,根据垂直得到90°的相等的角是解题的关键,也是本题容易忽视的条件.

练习册系列答案
相关题目
7. 如图,一个长方形绕轴l旋转一周得到的立体图形是( )
如图,一个长方形绕轴l旋转一周得到的立体图形是( )
 如图,一个长方形绕轴l旋转一周得到的立体图形是( )
如图,一个长方形绕轴l旋转一周得到的立体图形是( )| A. | 棱锥 | B. | 圆锥 | C. | 圆柱 | D. | 球 |
8.倒数等于它本身的数是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 0或±1 |
15.如果a、b互为相反数,且b≠0,则式子a+b,$\frac{a}{b}$,|a|-|b|的值分别为( )
| A. | 0,1,2 | B. | 1,0,1 | C. | 1,-1,0 | D. | 0,-1,0 |
12.方程2x2-3x+2=0的二次项系数和一次项系数分别为( )
| A. | 3和-2 | B. | 2和-3 | C. | 2和3 | D. | -3和2 |

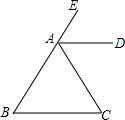 如图,已知:AD平分∠CAE,AD∥BC.
如图,已知:AD平分∠CAE,AD∥BC.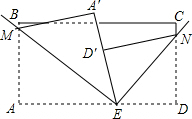 如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.
如图,长方形纸片ABCD,点E为AD边上的点,将纸片先沿直线EM对折,对折后的点A的对应点为A′,再沿直线EN对阵,对折后点D的对应点为D′,并且D′刚好落在A′E边上.