如图.将长方形纸片ABCD折叠.使点D与点B重合.折痕为EF．已知AB=6cm.BC=18cm.则Rt△ABE的面积为( )A．27cm2B．24cm2C．22cm2D．20cm2 题目和参考答案——青夏教育精英家教网—

题目内容

13．

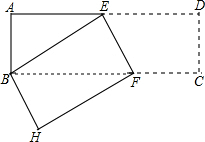如图，将长方形纸片ABCD折叠，使点D与点B重合，折痕为EF．已知AB=6cm，BC=18cm，则Rt△ABE的面积为（　　）

A．

27cm²

B．

24cm²

C．

22cm²

D．

20cm²

分析设AE=xcm，根据折叠的性质得出ED=BE=（18-x）cm，在Rt△ABE中根据勾股定理可得6²+x²=（18-x）²，解方程求出AE的长，从而不难求得△ABE的面积．

解答解：设AE=xcm，由折叠可知：ED=BE=（18-x）cm，
∵在Rt△ABE中，6²+x²=（18-x）²，
∴x=8，
∴S_△ABE=$\frac{1}{2}$AE•AB=$\frac{1}{2}$×8×6=24（cm²）．
故选B．

点评此题考查了折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．也考查了勾股定理和三角形的面积，求出AE的长是解题的关键．

练习册系列答案

相关题目

3．

如图，△ABC中，∠ACB=90°，沿CD边折叠△CBD，使点B恰好落在AC边上的点E处，若∠A=22°，则∠BDC等于67°．

4．

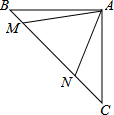如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°．若BM=1，CN=3，则MN的长为$\sqrt{10}$．

1．

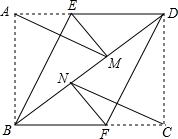在矩形ABCD中，将点A翻折到对角线BD上的点M处，折痕BE交AD于点E．将点C翻折到对角线BD上的点N处，折痕DF交BC于点F．
（1）求证：四边形BFDE为平行四边形；
（2）若四边形BFDE为菱形，且AB=1，求BC的长．

8．

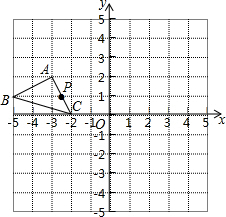如图，在10×10的正方形网格中，每个小正方形的边长均为1个单位．平面直角坐标系和△ABC的位置如图所示．
（1）画出△ABC关于（-1，-1）的中心对称△A₁B₁C₁；
（2）P（a，b）是△ABC的边AC上一点，△ABC经平移后点P的对应点为Q（a+6，b+2），请画出上述平移后的△A₂B₂C₂，并写出点A₂、C₂的坐标．

18．请阅读下列材料：
问题：如图（1），圆柱的底面半径为4cm，圆柱高AB为2cm，BC是底面直径，求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线，小明设计了两条路线：
路线1：高线AB+底面直径BC，如图（1）所示．
路线2：侧面展开图中的线段AC，如图（2）所示．

设路线1的长度为l₁，则l₁=AB+BC=2+8=10；
设路线2的长度为l₂，则l₂=$\sqrt{A{B^2}+B{C^2}}$=$\sqrt{{2^2}+{{（4π）}^2}}$=$\sqrt{4+16{π^2}}$；
∵${l_1}^2-{l_2}^2$=10²-（4+16π²）=96-16π²=16（6-π²）＜0
∴${l_1}^2＜{l_2}^2$即l₁＜l₂
所以选择路线1较短．
（1）小明对上述结论有些疑惑，于是他把条件改成：“圆柱的底面半径为2cm，高AB为4cm”继续按前面的路线进行计算．（结果保留π）
①此时，路线1：l₁=8．路线2：l₂=$\sqrt{16+{4π}^{2}}$．
②所以选择哪条路线较短？试说明理由．
（2）请你帮小明继续研究：当圆柱的底面半径为2cm，高为hcm时，应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短．

5．

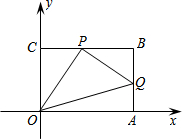已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（6，0）、C（0，4），点P在BC边上运动，过P作PQ⊥OP，交AB边于Q，则AQ的最小值为$\frac{7}{4}$．

2．分式方程$\frac{3}{x+2}=\frac{5}{x-1}$的解是$-\frac{13}{2}$．

3．

如图，点A、B、C为⊙O上的三点，连接AC，若∠ABC=130°，则∠OCA的度数为（　　）

试题分类