题目内容
13. 如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°.在楼顶C测得塔顶A的仰角30°.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.
如图,为了测量山顶铁塔AE的高,小明在27m高的楼CD底部D测得塔顶A的仰角为45°.在楼顶C测得塔顶A的仰角30°.已知山高BE为56m,楼的底部D与山脚在同一水平线上,求该铁塔的高AE.
分析 根据楼高和山高可求出EF,继而得出AF,在Rt△AFC中表示出CF,在Rt△ABD中表示出BD,根据CF=BD可建立方程,解出即可.
解答  解:如图,过点C作CF⊥AB于点F.
解:如图,过点C作CF⊥AB于点F.
设塔高AE=x,
由题意得,EF=BE-CD=56-27=29m,AF=AE+EF=(x+29)m,
在Rt△AFC中,∠ACF=30°,AF=(x+29)m,
则CF=$\frac{AF}{tan30°}$=$\frac{x+29}{\frac{\sqrt{3}}{3}}$=$\sqrt{3}$(x+29),
在Rt△ABD中,∠ADB=45°,AB=x+56,
则BD=AB=x+56,
∵CF=BD,
∴x+56=$\sqrt{3}$(x+29),
解得:x=$\frac{27\sqrt{3}-31}{2}$.
答:该铁塔的高AE为$\frac{27\sqrt{3}-31}{2}$米.
点评 本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,注意利用方程思想求解,难度一般.

练习册系列答案
相关题目
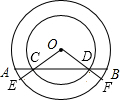 如图,以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,OC、OD的延长线交大圆于E、F.求证:$\widehat{AE}$=$\widehat{BF}$.
如图,以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,OC、OD的延长线交大圆于E、F.求证:$\widehat{AE}$=$\widehat{BF}$. 如图,在△ABC中,A(1,0),B(5,0),C(2,3),点D是BC上一点,且BD=2DC
如图,在△ABC中,A(1,0),B(5,0),C(2,3),点D是BC上一点,且BD=2DC 如图,探究∠A+∠B+∠C与∠ADC之间的关系,并说明理由.
如图,探究∠A+∠B+∠C与∠ADC之间的关系,并说明理由. 如图,是由一些大小相同的小正方体搭成的简单几何体.
如图,是由一些大小相同的小正方体搭成的简单几何体. 如图,桃花源管理处为了方便游客,决定在一条水平宽为100m,高为100m的山坡上铺设石板路,设AB是坡面,每块石板宽25cm(石板的厚度忽略不计),铺设方法如图所示,需购买这种石板多少块?
如图,桃花源管理处为了方便游客,决定在一条水平宽为100m,高为100m的山坡上铺设石板路,设AB是坡面,每块石板宽25cm(石板的厚度忽略不计),铺设方法如图所示,需购买这种石板多少块?