题目内容
16．计算：（1-$\frac{1}{{2}^{2}}$）（1-$\frac{1}{{3}^{2}}$）（1-$\frac{1}{{4}^{2}}$）…（1-$\frac{1}{19{8}^{2}}$）（1-$\frac{1}{19{9}^{2}}$）分析 利用平方差公式因式分解，进一步整理把分子分母交错约分抵消得出答案即可．
解答 解：原式=（1-$\frac{1}{2}$）（1+$\frac{1}{2}$）（1-$\frac{1}{3}$）（1+$\frac{1}{3}$）（1-$\frac{1}{4}$）（1+$\frac{1}{4}$）…（1-$\frac{1}{198}$）（1+$\frac{1}{198}$）（1-$\frac{1}{199}$）（1+$\frac{1}{199}$）
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{197}{198}$×$\frac{199}{198}$×$\frac{198}{199}$×$\frac{200}{199}$
=$\frac{1}{2}$×$\frac{200}{199}$
=$\frac{100}{199}$．
点评 此题考查因式分解的实际运用，掌握平方差公式是解决问题的关键．
练习册系列答案
相关题目
11．
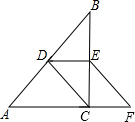如图，在Rt△ABC中，∠ACB=90°，点D、E分别为AB、BC的中点，点F在AC的延长线上，∠FEC=∠B．请问CF=DE成立吗？试说明理由．（提示：直角三角形斜边上的中线等于斜边的一半．）
如图，在Rt△ABC中，∠ACB=90°，点D、E分别为AB、BC的中点，点F在AC的延长线上，∠FEC=∠B．请问CF=DE成立吗？试说明理由．（提示：直角三角形斜边上的中线等于斜边的一半．）
1．
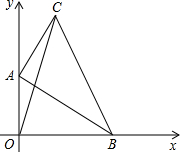如图，在平面直角坐标系中，Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动，若AB=4，AC=3，则在运动过程中，线段OC的最大值是（ ）
如图，在平面直角坐标系中，Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动，若AB=4，AC=3，则在运动过程中，线段OC的最大值是（ ）| A． | 5 | B． | 2+$\sqrt{13}$ | C． | $\sqrt{13}$ | D． | 6 |
如图，Rt△ABC中，∠ACB=90°，AC=BC，Rt△DEF中，∠DFE=90°，D、E两点分别在AC、BC上，且DE=BC．若∠CFB=135°，CF=1，EF=3，则AB=5$\sqrt{2}$．