题目内容
6.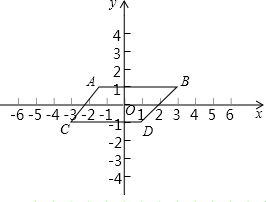 如图所示,平面直角坐标系中有一个平行四边形,点O是平行四边形ABCD对角线的交点,已知点A的坐标为(-1,1),点B的坐标为(3,1).
如图所示,平面直角坐标系中有一个平行四边形,点O是平行四边形ABCD对角线的交点,已知点A的坐标为(-1,1),点B的坐标为(3,1).(1)求点C、点D的坐标;
(2)平行四边形ABCD的周长是多少?
(3)求平行四边形ABCD各内角的度数是多少?
分析 (1)利用平行四边形是中心对称图形进而求出C,D点坐标即可;
(2)利用勾股定理得出以及两点之间距离求法得出即可;
(3)利用等腰直角三角形的性质结合平行四边形的性质得出内角度数即可.
解答 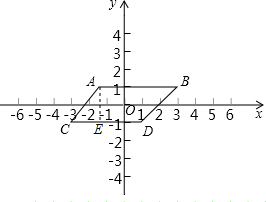 解:(1)∵平行四边形ABCD,点O是平行四边形ABCD对角线的交点,点A的坐标为(-1,1),点B的坐标为(3,1),
解:(1)∵平行四边形ABCD,点O是平行四边形ABCD对角线的交点,点A的坐标为(-1,1),点B的坐标为(3,1),
∴点C的坐标为:(-3,-1)、点D的坐标为:(1,-1);
(2)由(1)得:AB=3-(-1)=4,AC=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
故平行四边形ABCD的周长是:2(4+2$\sqrt{2}$)=8+4$\sqrt{2}$;
(3)过点A作AE⊥DC于点E,
∵点A的坐标为(-1,1),点C的坐标为:(-3,-1),
∴AE=2,EC=2,
∴∠C=45°,则∠CAB=135°,
故∠B=45°,∠D=135°.
点评 此题主要考查了平行四边形的性质以及勾股定理等知识,正确应用平行四边形的性质得出是解题关键.

练习册系列答案
相关题目
11.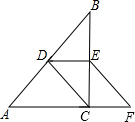 如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
 如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
如图,在Rt△ABC中,∠ACB=90°,点D、E分别为AB、BC的中点,点F在AC的延长线上,∠FEC=∠B.请问CF=DE成立吗?试说明理由.(提示:直角三角形斜边上的中线等于斜边的一半.)
4.计算(-2x+3y)(2x-3y)的结果为( )
| A. | -4x2+12xy-9y2 | B. | 4x2-9y2 | C. | 4x2-12xy+9y2 | D. | 9y2-4x2 |
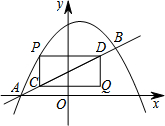 如图,抛物线$y=-\frac{1}{2}{x^2}+bx+c$与直线$y=\frac{1}{2}x+1$交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).
如图,抛物线$y=-\frac{1}{2}{x^2}+bx+c$与直线$y=\frac{1}{2}x+1$交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n). 如图所示,AB=DC,AD=BC,DE=BF,求证:BE=DF.
如图所示,AB=DC,AD=BC,DE=BF,求证:BE=DF. 如图,E、F分别为?ABCD的边AD、BC的中点,G、H在BD上,且BG=DH.求证:四边形EGFH是平行四边形.
如图,E、F分别为?ABCD的边AD、BC的中点,G、H在BD上,且BG=DH.求证:四边形EGFH是平行四边形.