题目内容
3. 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )| A. | 汽车共行驶了120千米 | |
| B. | 汽车在整个行驶过程中平均速度为40千米 | |
| C. | 汽车返回时的速度为80千米/时 | |
| D. | 汽车自出发后1.5小时至2小时之间速度不变 |
分析 横轴代表时间,纵轴代表行驶的路程,据此判断相应的路程和时间即可.
解答 解:A、由图象可以看出,最远处到达距离出发地120千米处,但又返回原地,所以行驶的路程为240千米,错误,不符合题意;
B、平均速度为总路程÷总时间,总路程为240千米,总时间为4.5小时,所以平均速度为240÷4.5≈53千米/时,故错误,不符合题意;
C、汽车返回所用的时间是1.5小时,则平均速度为:$\frac{120}{1.5}$=80(千米/时),正确,符合题意;
D、汽车自出发后3小时至4.5小时之间行驶的速度不变,故错误,不符合题意;
故选:C.
点评 本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决;用到的知识点为:平均速度=总路程÷总时间.

练习册系列答案
相关题目
14.某商场第一季度的总利润是100万元,其中一月份的利润是20万元,设平均每月利润增长率为x,则依题意列出方程为( )
| A. | 20(1+x)2=100 | B. | 20+20x+20x2=100 | ||
| C. | 20+20(1+x)+20(1+x)2=100 | D. | 20(1+x)=100 |
11.2014年某市提出了总计约2450万元的投资计划,将2450万用科学记数法表示应为( )
| A. | 2.45×103 | B. | 2.45×106 | C. | 0.245×107 | D. | 2.45×107 |
18.下列命题中真命题是( )
| A. | 以40°角为内角的两个等腰三角形必定相似 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 一组对边平行,另一组对边相等的四边形是平行四边形 | |
| D. | 有两个角和其中一个角的对边对应相等的两个三角形全等 |
15.已知点P位于第二象限,到y轴的距离是5,到x轴的距离是4,则点P坐标是( )
| A. | (-5,4) | B. | (5,4) | C. | (-4,5) | D. | (4,5) |
12.与点P(-3,4)关于原点对称的点Q的坐标为( )
| A. | (-3,-4) | B. | (3,-4) | C. | (3,4) | D. | (4,-3) |
13.已知二次函数y=mx2-3mx-4m(m≠0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C且∠ACB=90°,则m的值为( )
| A. | ±2 | B. | ±4 | C. | ±$\frac{1}{2}$ | D. | ±$\frac{1}{4}$ |
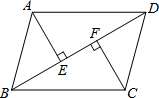 如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.
如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$. 如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.
如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD.