题目内容
13.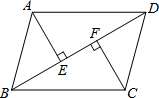 如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.
如图,平行四边形ABCD中,AE⊥BD于E,CF⊥BD于F,∠ABC=75°,∠DBC=30°,BC=2,则BD的长度为1+$\sqrt{3}$.
分析 利用平行四边形的性质得出AD=BC,再利用全等三角形的判定方法得出△ADE≌△CBF,得出DE=BF,求出BE、DE即可解决问题.
解答 (1)证明:在?ABCD中,AD∥BC,AD=BC.
则∠ADE=∠CBF.
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AED=∠CFB=90°.
在△ADE和△CBF中,
$\left\{\begin{array}{l}{∠AED=∠BFC}\\{∠ADE=∠CBF}\\{AD=BC}\end{array}\right.$,
∴△ADE≌△CBF(AAS).
∴DE=BF.
∵∠ABC=75°,∠DBC=30°,
∴∠ABE=75°-30°=45°.
∵AB∥CD,
∴∠ABE=75°-30°=45°
∵AD=BC=2,∠ADE=∠CBF=30°,
∴在Rt△ADE中,AE=1,
DE=$\sqrt{4-1}$=$\sqrt{3}$.
在Rt△AEB中,∠ABE=∠BAE=45°
故AE=BE=1.
∴BD=BE+DE=1+$\sqrt{3}$.
故答案为1+$\sqrt{3}$.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质和勾股定理等知识,得出△ADE≌△CBF是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{16}$=±4 | B. | ($\frac{1}{2}$)-1=-2 | C. | 20=0 | D. | |-6|=6 |
1.某市举行中小学生器乐交流比赛,有45支队伍参赛,他们参赛的成绩各不相同,要取前23名获奖,某代表队已经知道了自己的成绩,他们想知道自己是否获奖,只需再知道这45支队伍成绩的( )
| A. | 中位数 | B. | 平均数 | C. | 最高分 | D. | 方差 |
8.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\frac{\sqrt{18}-\sqrt{8}}{2}$=$\sqrt{9}$-$\sqrt{4}$ |
5.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a2=a3 | C. | (a2)3=a6 | D. | 2a2×3a=6a2 |
3. 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )| A. | 汽车共行驶了120千米 | |
| B. | 汽车在整个行驶过程中平均速度为40千米 | |
| C. | 汽车返回时的速度为80千米/时 | |
| D. | 汽车自出发后1.5小时至2小时之间速度不变 |