题目内容
14.某商场第一季度的总利润是100万元,其中一月份的利润是20万元,设平均每月利润增长率为x,则依题意列出方程为( )| A. | 20(1+x)2=100 | B. | 20+20x+20x2=100 | ||
| C. | 20+20(1+x)+20(1+x)2=100 | D. | 20(1+x)=100 |
分析 主要考查增长率问题,一般用增长后的量=增长前的量×(1+增长率),如果设利润平均每月的增长率为x,根据“第一季度的利润是100万元”,可得出方程
解答 解:设利润平均每月的增长率为x,
又知:第一季度的总利润是100万元,其中一月份的利润是20万元,
所以,可列方程为:20+20(1+x)+20(1+x)2=100;
故选:C.
点评 本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b(当增长时中间的“±”号选“+”,当降低时中间的“±”号选“-”).

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
4.下列计算正确的是( )
| A. | $\sqrt{16}$=±4 | B. | ($\frac{1}{2}$)-1=-2 | C. | 20=0 | D. | |-6|=6 |
5.下列计算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a2=a3 | C. | (a2)3=a6 | D. | 2a2×3a=6a2 |
9.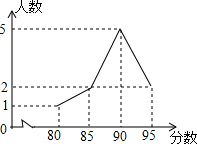 在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
 在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )
在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( )| A. | 众数是90 | B. | 中位数是90 | C. | 平均数是89 | D. | 平均数是87.5 |
19.在平面直角坐标系中,点A(-1,3)关于原点O对称的点A′的坐标为( )
| A. | (1,3) | B. | (1,-3) | C. | (3,1) | D. | (-1,-3) |
3. 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
 如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )
如图,图象(折线ABCDE)描述了一汽车在某一直线上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,给出下列说法,其中正确的说法是( )| A. | 汽车共行驶了120千米 | |
| B. | 汽车在整个行驶过程中平均速度为40千米 | |
| C. | 汽车返回时的速度为80千米/时 | |
| D. | 汽车自出发后1.5小时至2小时之间速度不变 |
4.一个三角形的两边长分别为3和7,第三边长为整数,则第三边长度的最小值是( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
 如图是用小正方体搭成的几何体的主视图和俯视图,俯视图上的数字表示小正方体的个数,则搭这个几何体最多要( )个小正方体.
如图是用小正方体搭成的几何体的主视图和俯视图,俯视图上的数字表示小正方体的个数,则搭这个几何体最多要( )个小正方体.