题目内容
7.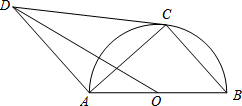 如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连接OD、AC.若tanB=$\frac{\sqrt{5}}{2}$,OD=3$\sqrt{6}$,则⊙O的半径为3.
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,AD∥BC,连接OD、AC.若tanB=$\frac{\sqrt{5}}{2}$,OD=3$\sqrt{6}$,则⊙O的半径为3.
分析 由已知条件和圆周角定理易证△CAB∽△DAC,由AC:BC的值可设AC=$\sqrt{5}$k,则BC=2k,由勾股定理可得AB=3k,继而表示出DC的长,然后由勾股定理建立关于k的方程,解方程即可得到问题答案.
解答 证明:连结OC.
∵AB是⊙O的直径,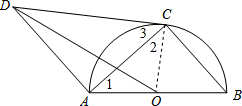
∴∠ACB=90°,
∴∠1+∠B=90°,
又∵OA=OC,
∴∠1=∠2,
∴∠2+∠B=90°,
∵∠DCA=∠B,
∴∠3+∠2=90°,
∵AD∥BC,AB是⊙O的直径,
∴∠DAC=∠ACB=90°,
∵∠1+∠B=90°,∠2+∠3=90°,∠1=∠2,
∴∠B=∠3,
∴△CAB∽△DAC,
∴$\frac{AC}{DA}$=$\frac{BC}{AC}$=$\frac{AB}{DC}$,
∵$\frac{AC}{BC}$=$\frac{\sqrt{5}}{2}$,
∴设AC=$\sqrt{5}$k,BC=2k,则AB=3k,
∴$\frac{3k}{DC}$=$\frac{2k}{\sqrt{5}k}$,
∴DC=$\frac{3\sqrt{5}}{2}$k,
在△ODC中,OD=3 $\sqrt{6}$,OC=$\frac{1}{2}$AB=$\frac{3}{2}$k,
∴(3 $\sqrt{6}$)2=( $\frac{3}{2}$k)2+( $\frac{3\sqrt{5}}{2}$k)2,
∴解得:k=2,
∴AB=3k=6,
∴⊙O的半径为3.
故答案为3.
点评 此题考查了切线的性质、相似三角形的判定与性质以及勾股定理等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
15.某工厂用A,B两种原件组装成C,D两种产品,组装一件C产品需1个A原件和4个原件;组装一件D产品需2个A原件和3个B原件.
(1)现有A原件162个,B原件340个,若要组装C,D两种产品共100个,设组装C产品x个.
①根据题意,完成下面表格:
②按两种产品的生产件数来分,有哪几种生产方案?
(2)现有A原件162个,B原件a个,组装C,D两种产品,A,B两种原件均恰好用完,已知290<a<306,求a的值.
(1)现有A原件162个,B原件340个,若要组装C,D两种产品共100个,设组装C产品x个.
①根据题意,完成下面表格:
| 原件 产品 | C(件) | D(件) |
| A(个) | x | 2(100-x) |
| B(个) | 4x | 3(100-x) |
(2)现有A原件162个,B原件a个,组装C,D两种产品,A,B两种原件均恰好用完,已知290<a<306,求a的值.