题目内容
2．已知方程x2+2009x+1=0的两根为α、β，则式子（α2+2008α+1）（β2+2010β+1）的值为-1．分析 由一元二次方程的解以及根与系数的关系，可得出α2+2009α+1=0、β2+2009β+1=0、α•β=1，将其代入（α2+2008α+1）（β2+2010β+1）=（α2+2009α+1-α）（β2+2009β+1+β）中即可求出结论．
解答 解：∵方程x2+2009x+1=0的两根为α、β，
∴α2+2009α+1=0，β2+2009β+1=0，αβ=1，
∴（α2+2008α+1）（β2+2010β+1）=（α2+2009α+1-α）（β2+2009β+1+β）=（-α）β=-αβ=-1．
故答案为：-1．
点评 本题考查了根与系数的关系以及一元二次方程的解，根据一元二次方程的解结合根与系数的关系找出α2+2009α+1=0、β2+2009β+1=0、α•β=1是解题的关键．
练习册系列答案
相关题目
如图．将三角形ABC绕着点C按顺时针方向旋转20°，B点落在B′位置，A点落在A′位置，则∠BCB′的度数是20°．
17．
如图，矩形ABCD中，E、H、F、G为AD、AB、BC、CD边上的点，连结OC、CH，CH交EF于I，EF∥AB，GH∥AD，EF、GH交于O点，如果AE：ED=2：3，AH：HB=1：4，S△OCI=1，则S矩形ABCD的值为（ ）
如图，矩形ABCD中，E、H、F、G为AD、AB、BC、CD边上的点，连结OC、CH，CH交EF于I，EF∥AB，GH∥AD，EF、GH交于O点，如果AE：ED=2：3，AH：HB=1：4，S△OCI=1，则S矩形ABCD的值为（ ）| A． | $\frac{125}{12}$ | B． | $\frac{125}{24}$ | C． | 40 | D． | 20 |
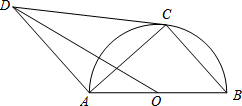如图，AB是⊙O的直径，点C在⊙O上，CD与⊙O相切，AD∥BC，连接OD、AC．若tanB=$\frac{\sqrt{5}}{2}$，OD=3$\sqrt{6}$，则⊙O的半径为3．
11．方程x2-x+2=0的根的情况（ ）
| A． | 有实根 | B． | 有两个相等实数根 | ||
| C． | 无实根 | D． | 有两个不相等实数根 |
