题目内容
设函数y=x+n的图象与y轴交于A点,函数y=-3x-m的图象与y轴交于B点,两个函数的图象交于C(-3,1)点,D为AB的中点.
(1)求m、n的值;
(2)求直线DC点的一次函数的表达式.
(1)求m、n的值;
(2)求直线DC点的一次函数的表达式.
考点:一次函数图象上点的坐标特征,待定系数法求一次函数解析式
专题:
分析:(1)直接把点C(-3,1)代入函数y=x+n与函数y=-3x-m,求出m、n的值即可;
(2)根据mn的值得出点A与点B的坐标,根据中点坐标公式求出D点坐标,利用待定系数法求出直线DC的函数解析式即可.
(2)根据mn的值得出点A与点B的坐标,根据中点坐标公式求出D点坐标,利用待定系数法求出直线DC的函数解析式即可.
解答:解:(1)∵函数y=x+n与函数y=-3x-m的图象交于C(-3,1)点,
∴1=-3+n,解得n=4;1=9-m,解得m=8,
∴n=4,m=8;
(2)∵函数y=x+n的图象与y轴交于A点,函数y=-3x-m的图象与y轴交于B点,
∴A(0,n),B(0,-m),
∵n=4,m=8,
∴A(0,4),B(0,-8).
∵D为AB的中点,
∴D(0,-2).
设直线CD的解析式为y=kx+b(k≠0),
∵C(-3,1),
∴
,解得
,
∴直线DC点的一次函数的表达式为y=-x-2.
∴1=-3+n,解得n=4;1=9-m,解得m=8,
∴n=4,m=8;
(2)∵函数y=x+n的图象与y轴交于A点,函数y=-3x-m的图象与y轴交于B点,
∴A(0,n),B(0,-m),
∵n=4,m=8,
∴A(0,4),B(0,-8).
∵D为AB的中点,
∴D(0,-2).
设直线CD的解析式为y=kx+b(k≠0),
∵C(-3,1),
∴
|
|
∴直线DC点的一次函数的表达式为y=-x-2.
点评:本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
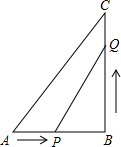 在△ABC中,∠B=90°,AB=6cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设P、Q分别从A、B同时出发,运动时间为t秒.
在△ABC中,∠B=90°,AB=6cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,设P、Q分别从A、B同时出发,运动时间为t秒.