题目内容
11.|x-3|+|y-5|=0,x+y=8,若|a|=|-5$\frac{1}{3}$|,则a=±5$\frac{1}{3}$.分析 根据非负数的性质列方程求出x、y的值,然后相加计算即可得解;
根据绝对值的性质解答即可.
解答 解:由题意得,x-3=0,y-5=0,
解得x=3,y=5,
所以,x+y=3+5=8,
∵|a|=|-5$\frac{1}{3}$|=5$\frac{1}{3}$,
∴a=±5$\frac{1}{3}$.
故答案为:8;±5$\frac{1}{3}$.
点评 本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0,还考查了绝对值的性质.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
6.一个数的相反数不比它本身大,则这个数为( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
16.下列说法中,正确的是( )
| A. | 0是最小的自然数,最大的负数是-1 | |
| B. | 绝对值等于它本身的数是0和1 | |
| C. | 任何有理数的绝对值都是正数 | |
| D. | 任何有理数的绝对值都不可能小于0 |
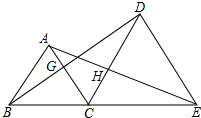 如图,已知△ABC和△DCE都是等边三角形(三边都相等,三个角都是60°),且B,C,E在同一直线上,连接BD交AC于点G,连接AE交CD于点H.求证:
如图,已知△ABC和△DCE都是等边三角形(三边都相等,三个角都是60°),且B,C,E在同一直线上,连接BD交AC于点G,连接AE交CD于点H.求证: