题目内容
4.在矩形ABCD中,对角线长为6,有一边长为3,点P为直线AD上一动点(与点A、D不重合),若∠ABP=30°,则DP的长为2$\sqrt{3}$.分析 由矩形的性质得出∠A=90°,AB=3,BD=6=2AB,求出∠ADB=30°=∠ABP,得出DP=BP,BP=2AP,由三角函数求出AP得出BP,即可得出结果.
解答 解:如图所示: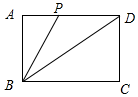
∵四边形ABCD是矩形,
∴∠A=90°,AB=3,BD=6=2AB,
∴∠ADB=30°=∠ABP,
∴DP=BP,BP=2AP,
∵AP=AB•tan30°=$\sqrt{3}$,
∴BP=2$\sqrt{3}$,
∴DP=2$\sqrt{3}$;
故答案为:2$\sqrt{3}$.
点评 本题考查了矩形的性质、含30°角的直角三角形的性质、等腰三角形的判定、三角函数等知识;熟练掌握矩形的性质,证出DP=BP是关键.

练习册系列答案
相关题目
19.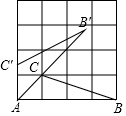 如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
 如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )
如图,点A、B、C均在边长为1的正方形网格的格点上,将△ABC绕着点A逆时针方向旋转得到△AB′C′,若使AB′经过点C,则$\widehat{B′B}$的长为( )| A. | $\frac{π}{2}$ | B. | π | C. | 6π | D. | 7π |
6.一个数的相反数不比它本身大,则这个数为( )
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
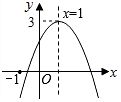 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论: