题目内容
1.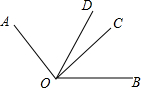 如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.
如图,OD是∠AOB的平分线,∠AOC=2∠BOC,∠COD=21°20′,求∠AOB的度数.
分析 设∠BOC=x,然后用x与∠COD的度数分别表示出∠AOD与∠BOD,然后根据角平分线的定义可知∠AOD=∠BOD,计算即可求出x的值,然后求出∠AOC与∠BOC的度数,相加即可得解.
解答 解:设∠BOC=x,则∠AOC=2x,
∵∠COD=21°20′,
∴∠AOD=2x-21°20′,∠BOD=x+21°20′,
∵OD是∠AOB的平分线,
∴∠AOD=∠BOD,
∴2x-21°20′=x+21°20′,
解得x=42°40′,
∴2x=2×42°40′=85°20′,
即∠AOC=85°20′,∠BOC=42°40′,
∴∠AOB=∠AOC+∠BOC=85°20′+42°40′=128°.
点评 本题主要考查了角度的计算,角平分线的定义,分别表示出∠AOD与∠BOD是解题的关键,需要注意度、分、秒是60进制,计算时不要出错.

练习册系列答案
相关题目
6.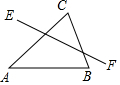 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )| A. | 4$\sqrt{6}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |