题目内容
12.如图1,直线y=-$\frac{\sqrt{3}}{3}$x+2$\sqrt{3}$分别与x轴、y轴交于点M,N.Rt△ABC的顶点B与原点O重合,BC在x轴正半轴上,BC=1,∠ABC=60°.将△ABC沿x轴正方向以每秒1个单位长度的速度平移,当点B与点M重合时,△ABC停止运动,设运动时间为t秒.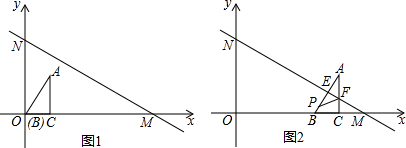
(1)当点A落在直线MN上时,求t的值;
(2)在(1)基础上,△ABC继续平移,AB,AC分别交线段MN于点E,F(如图2).
①t为何值时,S△AEF=$\frac{1}{2}$S△ABC;
②若当点A刚好落在直线MN上时,动点P同时从顶点B出发,以每秒$\frac{1}{2}$个单位长度的速度沿B→A运动,△ABC停止平移时,点P随之停止.则在点P运动的过程中,是否存在某一时刻,△PEF与△MON相似?若存在,求出此时t的值;若不存在,请说明理由.
分析 (1)根据函数解析式易求ON、OM的值,以及∠NMO=30°,在Rt△ABC中,根据∠NMO=30°,可得BM=2AB,由BM=6-t,AB=2,可求得t的值;
(2)①根据BM=6-t,AB⊥NM,分别表示出BE、AE、EF的长度,然后根据S△AEF=$\frac{1}{2}$S△ABC,代入三角形的面积公式,求出t的值;
②根据图形可得,分别表示出当2≤t≤4时,即当点P在BE上,当4≤t≤6时,即当点P在AE上时PE的长度,然后根据角度的不同分情况,求出t的值.
解答 解:(1)根据函数解析式易求ON=2$\sqrt{3}$,OM=6,∠NMO=30°,
在Rt△ABC中,∠ABC=60°,BC=1,
∴AB=2,AC=$\sqrt{3}$,
当点A在MN上时,
∵∠ABC=60°,∠NMO=30°,
∴AB⊥NM,
∴BM=2AB,
由BM=6-t,AB=2,
可得6-t=4,
解得:t=2;
(2)①如图2,
∵BM=6-t,AB⊥NM,
∴BE=$\frac{1}{2}$BM=$\frac{1}{2}$(6-t)=3-$\frac{1}{2}$t,
∴AE=AB-BE=2-(3-$\frac{1}{2}$t)=$\frac{1}{2}$t-1,
∴EF=AE•tan30°=$\frac{\sqrt{3}t-2\sqrt{3}}{6}$,
∵S△AEF=$\frac{1}{2}$S△ABC,
∴($\frac{1}{2}$t-1)×$\frac{\frac{1}{2}t-1}{\sqrt{3}}$×$\frac{1}{2}$=$\frac{1}{2}$×$\frac{\sqrt{3}}{2}$,
解得:t1=2+$\sqrt{6}$,t2=2-$\sqrt{6}$(不合题意,舍去);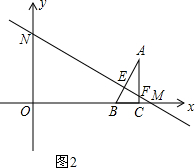 ②PE=3-$\frac{1}{2}$t-$\frac{1}{2}$(t-2)=4-t(2≤t≤4),
②PE=3-$\frac{1}{2}$t-$\frac{1}{2}$(t-2)=4-t(2≤t≤4),
或PE=$\frac{1}{2}$(t-2)-(3-$\frac{1}{2}$t)=t-4(4≤t≤6),
要使△PEF与△OMN相似,
即△PEF为含有30°的直角三角形,而∠PEF始终为直角.
(i)当点P在BE上,即当2≤t≤4时,
若∠PFE=30°,
则$\sqrt{3}$(4-t)=$\frac{\sqrt{3}t-2\sqrt{3}}{6}$,
解得:t=$\frac{26}{7}$;
若∠EPF=30°,
则4-t=$\frac{\sqrt{3}t-2\sqrt{3}}{6}$×$\sqrt{3}$,
解得:t=$\frac{10}{3}$;
(ii)当点P在AE上,即当4≤t≤6时,
若∠PFE=30°,
则$\sqrt{3}$(t-4)=$\frac{\sqrt{3}t-2\sqrt{3}}{6}$,
解得:t=$\frac{22}{5}$;
若∠EPF=30°,
则t-4=$\frac{\sqrt{3}t-2\sqrt{3}}{6}$×$\sqrt{3}$,
解得:t=6;
而当t=6时,点P和点A重合,AC与线段MN没有交点,
所以t=6不合题意舍去,
综上所述,当t1=$\frac{26}{7}$,t2=$\frac{10}{3}$,t3=$\frac{22}{5}$时,△PEF与△MON相似.
点评 此题考查了一次函数的综合应用,涉及到含30度角的直角三角形、三角形的面积,相似三角形的判定与性质,勾股定理等知识点,综合性强,难度较大,尤其是动点问题,给此题增加了一定的难度,此题属于难题.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案| A. | 2$\sqrt{5}$×3$\sqrt{5}$=6×25=150 | B. | 2$\sqrt{5}$×3$\sqrt{5}$=6×5=30 | C. | 2$\sqrt{5}$×3$\sqrt{5}$=6$\sqrt{5}$ | D. | 2$\sqrt{5}$×3$\sqrt{5}$=5$\sqrt{5}$ |

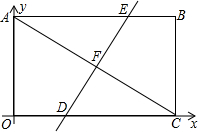 如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,
如图,平面直角坐标系中,矩形OABC的对角线AB=8,BC=4,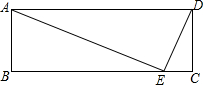 如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n,且m、n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2,试求BE的长.
如图,在矩形ABCD中,E为BC上一点,AE⊥DE,∠DAE=30°,若DE=m+n,且m、n满足m=$\sqrt{n-8}$+$\sqrt{16-2n}$+2,试求BE的长.