题目内容
4.当m<2时,函数y=2x-2m+4的图象与x轴交于负半轴.分析 根据k大于零,b大于零时,图象经过一、二、三象限,即此时图象与x轴的负半轴相交,可得答案.
解答 解:∵函数y=2x-2m+4的图象与x轴交于负半轴,
∴-2m+4>0,
解得:m<2,
故答案为:<2.
点评 本题考查的是一次函数的图象与系数的关系,熟知一次函数y=kx+b(k≠0)中,当k>0,b<0时,函数的图象经过一、三、四象限是解答此题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
19.在某样本方差的计算公式s2=$\frac{1}{10}$[(x1-8)2+(x2-8)2+…+(x10-8)2]中,数字10和8依次表示样本的( )
| A. | 容量,方差 | B. | 平均数,容量 | C. | 容量,平均数 | D. | 方差、平均数 |
13.大学生小东到某快递公司做社会调查,了解到该快递公司为激励业务员的工作积极性,实行“月工资=基本工资+计件奖金”的办法,(计件奖金=月取送件数×每件奖金),并获得如下信息:
(1)求业务员的月基本工资和取送每件的奖金;
(2)若营业员丙月工资不低于2470元,这位营业员当月至少要取送多少件?
| 业务员 | 甲 | 乙 |
| 月取送件数/件 | 1200 | 900 |
| 月总收入/元 | 1920 | 1590 |
(2)若营业员丙月工资不低于2470元,这位营业员当月至少要取送多少件?
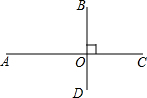 如图,已知线段AC、BD相互垂直,垂足为O,且OA>OC,OB>OD.
如图,已知线段AC、BD相互垂直,垂足为O,且OA>OC,OB>OD.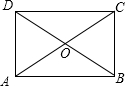 如图,矩形ABCD的对角线AC,BD交于点O,∠AOD=60°,AD=3,则BD的长为6.
如图,矩形ABCD的对角线AC,BD交于点O,∠AOD=60°,AD=3,则BD的长为6.