题目内容
4.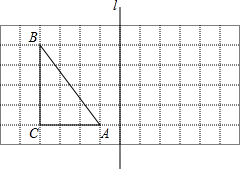 如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.
如图,在边长为1个单位长度的小正方形所组成的网格中,△ABC的顶点均在格点上.①sinB的值是$\frac{3}{5}$;
②画出△ABC关于直线l对称的△A1B1C1(A与A1,B与B1,C与C1相对应).连接AA1,BB1,并计算梯形AA1B1B的面积.
分析 ①利用勾股定理得出AB的长,再利用锐角三角函数关系得出答案;
②利用关于直线对称的性质得出对应点进而利用梯形面积求法得出答案.
解答  解:①∵AC=3,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
解:①∵AC=3,AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴sinB的值是:$\frac{AC}{AB}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$;
②如图所示:△A1B1C1,即为所求,
梯形AA1B1B的面积为:$\frac{1}{2}$×(2+8)×4=20.
点评 此题主要考查了轴对称变换和勾股定理以及锐角三角函数关系,正确掌握梯形面积公式是解题关键.

练习册系列答案
相关题目
15.把x2y-2y2x+y3分解因式正确的是( )
| A. | y(x+y)(x-y) | B. | y(x-y)2 | C. | y(x2-2xy+y2) | D. | (x-2y)2 |
9.-32的相反数是( )
| A. | 6 | B. | -6 | C. | 9 | D. | -9 |
13.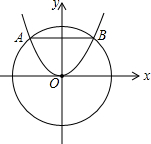 如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )
如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )
 如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )
如图,⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4,则⊙O的半径为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 4 |
14.关于x的不等式(a-1)x-1>0的解集是x<b,则b与a的关系式为( )
| A. | b=$\frac{1}{a-1}$ | B. | b=-$\frac{1}{a-1}$ | C. | b=a-1 | D. | b=-a+1 |