题目内容
1．
如图，Rt△ABC绕着点A顺时针旋转90°得到△AB′C′，若∠B=25°，∠C=90°．则∠BAC′的度数是25°．
分析 先根据旋转的性质得∠CAC′=90°，加上∠C=90°，则可判断BC∥AC′，然后根据平行线的性质求解．
解答 解：∵△ABC绕着点A顺时针旋转90°得到△AB′C′，
∴∠CAC′=90°，
而∠C=90°，
∴BC∥AC′，
∴∠BAC′=∠B=25°．
故答案为25°．
点评 本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．
练习册系列答案
相关题目
11．若-3+（ ）=0，则（ ）中的数应该是（ ）
| A． | 3 | B． | -3 | C． | $-\frac{1}{3}$ | D． | $\frac{1}{3}$ |
9．-32的相反数是（ ）
| A． | 6 | B． | -6 | C． | 9 | D． | -9 |
13．
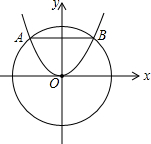如图，⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4，则⊙O的半径为（ ）
如图，⊙O被抛物线y=$\frac{1}{2}$x2所截的弦长AB=4，则⊙O的半径为（ ）| A． | 2 | B． | 2$\sqrt{2}$ | C． | $\sqrt{5}$ | D． | 4 |
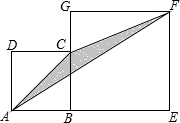如图，四边形ABCD和四边形BEFG均为正方形，且A、B、E三点共线，正方形ABCD的边长为4，则S△ACF的面积为8．