题目内容
9.在△ABC中,AB=$\sqrt{5}$,AC=2,BC=3.(1)求该三角形外接圆的面积;
(2)将△ABC绕AC所在直线旋转一周,求所得几何体的表面积.
分析 由勾股定理的逆定理证得△ABC为直角三角形,则三角形外接圆的直径为△ABC的斜边BC,由圆的面积公式即可求得结论;
(2)易得此几何体为是底面圆半径是$\sqrt{5}$,母线是3的圆锥体,那么表面积为圆锥的侧面积与底面圆,圆锥的侧面积=底面周长×母线长÷2求解即可.
解答 解:(1)∵AB2+AC2=($\sqrt{5}$)2+22=9=BC2,
∴△BAC为直角三角形,
∴三角形外接圆的半径为$\frac{3}{2}$,
∴三角形外接圆的面积S=$\frac{9}{4}π$;
(2)求所得几何体是底面圆半径是$\sqrt{5}$,母线是3的圆锥体,
∴几何体的表面积=$\frac{1}{2}$×2$\sqrt{5}$×3π+($\sqrt{5}$)π=$(5+3\sqrt{5})π$.
点评 本题主要考查了勾股定理的逆定理,圆周角定理,圆的面积公式,圆锥的侧面积公式,能得到几何体的是解决本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20. 如图所示,正三棱柱的俯视图是( )
如图所示,正三棱柱的俯视图是( )
 如图所示,正三棱柱的俯视图是( )
如图所示,正三棱柱的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
18.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点(-1,2),则这个函数的图象一点经过( )
| A. | (-2,1) | B. | ($-\frac{1}{2}$,2) | C. | (-2,-1) | D. | ($\frac{1}{2}$,2) |
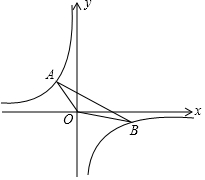 如图,点A(a,a+5)和点B(6,a+1)都在双曲线y=$\frac{k}{x}$(k<0)上.
如图,点A(a,a+5)和点B(6,a+1)都在双曲线y=$\frac{k}{x}$(k<0)上.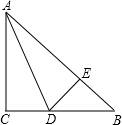 如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.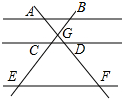 如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{BE}$的值等于$\frac{3}{8}$.
如图,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,那么$\frac{BC}{BE}$的值等于$\frac{3}{8}$.