题目内容
19.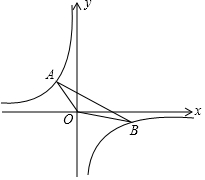 如图,点A(a,a+5)和点B(6,a+1)都在双曲线y=$\frac{k}{x}$(k<0)上.
如图,点A(a,a+5)和点B(6,a+1)都在双曲线y=$\frac{k}{x}$(k<0)上.(1)求k的值;
(2)求△AOB的面积.
分析 (1)由点A、B的坐标利用反比例函数图象上点的坐标特征即可得出关于a的一元二次方程,解之即可得出a值,将其代入k=a(a+5)中即可求出k值;
(2)根据a的值可找出点A、B的坐标,根据点A、B的坐标利用待定系数法即可求出直线AB的解析式,再根据一次函数图象上点的坐标特征即可找出点C的坐标,根据三角形的面积结合点A、B的横坐标即可求出△AOB的面积.
解答 解:(1)∵点A(a,a+5)和点B(6,a+1)都在双曲线y=$\frac{k}{x}$(k<0)上,
∴k=a(a+5)=6(a+1),整理得:a2-a-6=(a+2)(a-3)=0,
解得:a=-2或a=3(舍去),
∴k=a(a+5)=-2×(-2+5)=-6.
(2)∵a=-2,
∴A(-2,3),B(6,-1).
设直线AB的解析式为y=kx+b(k≠0),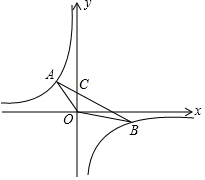
将A(-2,3)、B(6,-1)代入y=kx+b中,
$\left\{\begin{array}{l}{-2k+b=3}\\{6k+b=-1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-$\frac{1}{2}$x+2.
设直线AB与y轴交于点C,则点C的坐标为(0,2),
∴OC=2,
∴S△AOB=$\frac{1}{2}$OC•(xB-xA)=$\frac{1}{2}$×2×[6-(-2)]=8.
点评 本题考查了一次函数图象上点的坐标特征、因式分解法解一元二次方程、反比例函数图象上点的坐标特征以及待定系数法求一次函数解析式,解题的关键是:(1)根据反比例函数图象上点的坐标特征找出关于a的一元二次方程;(2)根据点A、B的坐标利用待定系数法求出直线AB的解析式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 3$\sqrt{3}$ | B. | 6 | C. | 3 | D. | $\sqrt{3}$ |
 将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( )
将一个三角形和一个矩形按照如图的方式扩大,使他们的对应边之间的距离均为1,得到新的三角形和矩形,下列说法正确的是 ( )| A. | 新三角形与原三角形相似 | |
| B. | 新矩形与原矩形相似 | |
| C. | 新三角形与原三角形、新矩形与原矩形都相似 | |
| D. | 都不相似 |