题目内容
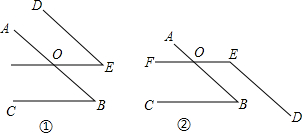
 已知:如图,已知AB∥CD,AD,BC交于点E,F为BC上一点,且∠EAF=∠C,若AF=6,EF=4,求BE的长.
已知:如图,已知AB∥CD,AD,BC交于点E,F为BC上一点,且∠EAF=∠C,若AF=6,EF=4,求BE的长.考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:先证∠B=∠EAF,再由公共角相等,证明△AFE∽△BFA,得出比例式
=
,求出BF=
=9,即可求出BE的长.
| AF |
| BF |
| EF |
| AF |
| AF2 |
| EF |
解答:证明:∵AB∥CD(已知),
∴∠B=∠C(两直线平行内错角相等),
又∵∠EAF=∠C(已知),
∴∠B=∠EAF(等量代换),
又∵∠AFE=∠BFA(公共角),
∴△AFE∽△BFA(两对对应角相等的两三角形相似),
∴
=
(相似三角形的对应边成比例),
∴BF=
=
=9,
∴BE=BF-EF=9-4=5.
∴∠B=∠C(两直线平行内错角相等),
又∵∠EAF=∠C(已知),
∴∠B=∠EAF(等量代换),
又∵∠AFE=∠BFA(公共角),
∴△AFE∽△BFA(两对对应角相等的两三角形相似),
∴
| AF |
| BF |
| EF |
| AF |
∴BF=
| AF2 |
| EF |
| 62 |
| 4 |
∴BE=BF-EF=9-4=5.
点评:此题考查了相似三角形的判定与性质以及平行线的性质;证明三角形相似得出比例式是解决问题的关键.

练习册系列答案
相关题目
 如图,已知:AB是⊙O的直径,C、D是弧
如图,已知:AB是⊙O的直径,C、D是弧 |
| AB |
| A、150° | B、135° |
| C、140° | D、120° |
 如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF
如图,点O是?ABCD对角线AC中点,EF经过点O交AD于点E,交BC于点F,连接BE,DF 有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由.
有一块形状为平行四边形的铁片,用AB表示较长的一边,AD、BC表示较短的边,现有AB=2AD.现在想用这块铁片截一个直角三角形,并且希望以AB为斜边,直角顶点在CD上,问此想法是否可行?如果可行的话,请说明应该怎样截;如果不行,请说明理由. 如图,在△ABC中,AB=AC,∠BAC=90°,BC=8,⊙A与BC相切于点D,且与AB、AC分别交于点E、F,则劣弧
如图,在△ABC中,AB=AC,∠BAC=90°,BC=8,⊙A与BC相切于点D,且与AB、AC分别交于点E、F,则劣弧 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF.
如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF. 某宾馆要在一高BC=3m、长AB=5m、宽3m的楼梯上铺设地毯,楼梯的刨面如图所示.若地毯每平方米100元,则需要购买地毯的费用至少是
某宾馆要在一高BC=3m、长AB=5m、宽3m的楼梯上铺设地毯,楼梯的刨面如图所示.若地毯每平方米100元,则需要购买地毯的费用至少是 如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数
如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数