题目内容
 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF.
如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF.考点:相似三角形的判定
专题:证明题
分析:如图,证明∠ACF=∠BAC,此为解题的关键性结论;结合∠AFC=∠AFB,即可解决问题.
解答: 证明:如图,∵AD是∠BAC的平分线,
证明:如图,∵AD是∠BAC的平分线,
∴∠BAD=∠CAD(设为α);
∵EF⊥AD,且EF平分AD,
∴AF=DF,∠ADF=∠DAF;
∵∠ACF=∠ADF+α,∠BAC=∠DAF+α,
∴∠ACF=∠BAC,
∵∠AFC=∠AFB,
∴△ABF∽△CAF.
 证明:如图,∵AD是∠BAC的平分线,
证明:如图,∵AD是∠BAC的平分线,∴∠BAD=∠CAD(设为α);
∵EF⊥AD,且EF平分AD,
∴AF=DF,∠ADF=∠DAF;
∵∠ACF=∠ADF+α,∠BAC=∠DAF+α,
∴∠ACF=∠BAC,
∵∠AFC=∠AFB,
∴△ABF∽△CAF.
点评:该题主要考查了相似三角形的判定及其性质、角平分线的定义、线段垂直平分线的性质等几何知识点及其应用问题;解题的关键是牢固掌握相似三角形的判定及其性质.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB上的动点,E是BC上的动点,则AE+DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB上的动点,E是BC上的动点,则AE+DE的最小值为( )A、3+2
| ||
| B、10 | ||
C、
| ||
D、
|
 如图,正方形A,B,C,D的顶点ABCD都在坐标轴上,已知OA=OB=OC=OD=
如图,正方形A,B,C,D的顶点ABCD都在坐标轴上,已知OA=OB=OC=OD= 如图,菱形ABCD中,O为AC上一点,OA=AB,经过B、C、D三点的⊙O的半径为1,求cos∠AOB的值.
如图,菱形ABCD中,O为AC上一点,OA=AB,经过B、C、D三点的⊙O的半径为1,求cos∠AOB的值. 如图,公园内有一边长为20米的正方形空地,先要在阴影部分种上绿化,求阴影部分的面积.(结果保留三个有效数字)
如图,公园内有一边长为20米的正方形空地,先要在阴影部分种上绿化,求阴影部分的面积.(结果保留三个有效数字) 已知:如图,已知AB∥CD,AD,BC交于点E,F为BC上一点,且∠EAF=∠C,若AF=6,EF=4,求BE的长.
已知:如图,已知AB∥CD,AD,BC交于点E,F为BC上一点,且∠EAF=∠C,若AF=6,EF=4,求BE的长.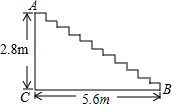 如图,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的价格为40元/m2,主楼梯的宽为3m,其侧面如图所示,则铺设这段楼梯至少需要多少元?
如图,某商场重新装修后,准备在大厅的主楼梯上铺设一种红色的地毯,已知这种地毯的价格为40元/m2,主楼梯的宽为3m,其侧面如图所示,则铺设这段楼梯至少需要多少元? (1)如图,已知∠B+∠D=∠BED,求证:AB∥CD,
(1)如图,已知∠B+∠D=∠BED,求证:AB∥CD, 如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.
如图所示,∠DAB=60°,CD⊥AD,CB⊥AB,且AB=2,CD=1,求AD和BC的长.