题目内容
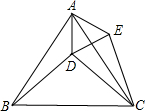 如图,D是等边△ABC内的一点,以AD为边向外作等边△ADE.
如图,D是等边△ABC内的一点,以AD为边向外作等边△ADE.(1)△ABD通过怎样的图形运动可以变成△ACE?(简要写出运动过程)
(2)若∠ADC=150°,CD=3,AD=4,求BD的长.
考点:旋转的性质,等边三角形的性质
专题:
分析:(1)由等边三角形的性质可得到∠DAE=60°,从而可得到△ABD通过逆时针旋转60°变成△ACE;
(2)利用旋转的性质得出BD=EC,利用已知得出∠EDC=90°,再利用勾股定理得出EC的长即可.
(2)利用旋转的性质得出BD=EC,利用已知得出∠EDC=90°,再利用勾股定理得出EC的长即可.
解答:解:(1)∵D是等边△ABC内的一点,以AD为边向外作等边△ADE,
∴AB=AC,AD=AE,∠DAE=60°,
∴△ABD通过逆时针旋转60°变成△ACE(也可以是顺时针旋转300°得到);
(2)∵△ABD通过逆时针旋转60°变成△ACE,
∴BD=EC,
∵∠ADC=150°,∠ADE=60°,
∴∠EDC=90°,
∵CD=3,AD=4,
∴DE=4,CD=3,
∴EC=BD=5.
∴AB=AC,AD=AE,∠DAE=60°,
∴△ABD通过逆时针旋转60°变成△ACE(也可以是顺时针旋转300°得到);

(2)∵△ABD通过逆时针旋转60°变成△ACE,
∴BD=EC,
∵∠ADC=150°,∠ADE=60°,
∴∠EDC=90°,
∵CD=3,AD=4,
∴DE=4,CD=3,
∴EC=BD=5.
点评:此题主要考查了勾股定理以及等边三角形的性质及旋转的性质的综合运用,得出BD=EC是解题关键.

练习册系列答案
相关题目
甲、乙两家汽车销售公司根据近几年的销售量分别制作如下统计
从2002~2006年,这两家公司中销售量增长较快的是( )公司.

从2002~2006年,这两家公司中销售量增长较快的是( )公司.
| A、甲公司 | B、乙公司 |
| C、一样快 | D、无法比较 |
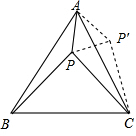 如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=
如图,等边△ABC内有一点P若点P到顶点A,B,C的距离分别为3,4,5,则∠APB=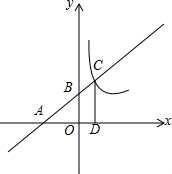 如图,在平面直角坐标系中,O为原点,直线y=
如图,在平面直角坐标系中,O为原点,直线y=