题目内容
3．y=$\sqrt{k-1}$x+1是关于x的一次函数，则一元二次方程kx2+2x+1=0的根的情况为（ ）| A． | 没有实数根 | B． | 有一个实数根 | ||
| C． | 有两个不相等的实数根 | D． | 有两个相等的实数根 |
分析 由一次函数的定义可求得k的取值范围，再根据一元二次方程的判别式可求得答案．
解答 解：
∵y=$\sqrt{k-1}$x+1是关于x的一次函数，
∴$\sqrt{k-1}$≠0，
∴k-1＞0，解得k＞1，
又一元二次方程kx2+2x+1=0的判别式△=4-4k，
∴△＜0，
∴一元二次方程kx2+2x+1=0无实数根，
故选A．
点评 本题主要考查一元二次方程根的判别式，掌握一元二次方程的根与判别式的关系是解题的关键，即①△＞0?一元二次方程有两个不相等的实数根，②△=0?一元二次方程有两个相等的实数根，③△＜0?一元二次方程无实数根．
练习册系列答案
相关题目
13．体育课上，老师测量跳远成绩的依据是（ ）
| A． | 垂直的定义 | B． | 两点之间线段最短 | ||
| C． | 垂线段最短 | D． | 两点确定一条直线 |
14．下列运算正确的是（ ）
| A． | 3$\sqrt{2}$-$\sqrt{2}$=3 | B． | a6÷a3=a2 | C． | a2+a3=a5 | D． | （3a3）2=9a6 |
11．货车行驶25千米与小车行驶35千米的时间相同，若小车的速度比货车的速度每小时快20千米，设货车的速度为x千米/小时，则根据题意，可列方程（ ）
| A． | $\frac{25}{x}$=$\frac{35}{x+20}$ | B． | $\frac{25}{x-20}$=$\frac{35}{x}$ | C． | $\frac{25}{x}$=$\frac{35}{x-20}$ | D． | $\frac{25}{x+20}$=$\frac{35}{x}$ |
8．
如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为（ ）
如图，△ABC中AB=AC=4，∠C=72°，D是AB中点，点E在AC上，DE⊥AB，则cosA的值为（ ）| A． | $\frac{\sqrt{5}-1}{2}$ | B． | $\frac{\sqrt{5}-1}{4}$ | C． | $\frac{\sqrt{5}+1}{4}$ | D． | $\frac{\sqrt{5}+1}{2}$ |
15．
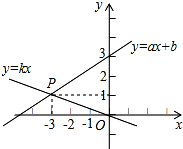如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x、y的二元一次方程组的解是（ ）
如图，已知函数y=ax+b和y=kx的图象交于点P，则根据图象可得，关于x、y的二元一次方程组的解是（ ）| A． | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
如图，直线a与直线b交于点A，与直线c交于点B，∠1=120°，∠2=35°，若使直线b与直线c平行，则可将直线b绕点A逆时针旋转25°．