题目内容
11.货车行驶25千米与小车行驶35千米的时间相同,若小车的速度比货车的速度每小时快20千米,设货车的速度为x千米/小时,则根据题意,可列方程( )| A. | $\frac{25}{x}$=$\frac{35}{x+20}$ | B. | $\frac{25}{x-20}$=$\frac{35}{x}$ | C. | $\frac{25}{x}$=$\frac{35}{x-20}$ | D. | $\frac{25}{x+20}$=$\frac{35}{x}$ |
分析 设货车的速度为x千米/小时,则小车的速度为(x+20)千米/小时,根据题意可得等量关系:货车行驶25千米的时间=小车行驶35千米的时间,根据等量关系列出方程即可.
解答 解:设货车的速度为x千米/小时,由题意得:
$\frac{25}{x}$=$\frac{35}{x+20}$,
故选:A.
点评 此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,表示出小车的速度,然后根据时间关系列出方程.

练习册系列答案
相关题目
1.一个正多边形的每个外角都是18°,这个正多边形的边数是( )
| A. | 9 | B. | 10 | C. | 19 | D. | 20 |
19. 如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )
如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )
 如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )
如图,平行四边形ABCD中,BD⊥AD,∠A=30°,BD=2,则CD的长为( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
16. 甲、乙同学沿着同一条笔直的路从A地骑自行车去B地,他们离出发地的距离s(km)和甲的行驶时间t(h)的函数关系如图,则下列说法中正确的个数为( )
甲、乙同学沿着同一条笔直的路从A地骑自行车去B地,他们离出发地的距离s(km)和甲的行驶时间t(h)的函数关系如图,则下列说法中正确的个数为( )
①他们都行使了18千米;
②甲在途中停留了0.5小时;
③乙比甲晚出发了0.5小时;
④甲、乙两人同时到达目的地.
 甲、乙同学沿着同一条笔直的路从A地骑自行车去B地,他们离出发地的距离s(km)和甲的行驶时间t(h)的函数关系如图,则下列说法中正确的个数为( )
甲、乙同学沿着同一条笔直的路从A地骑自行车去B地,他们离出发地的距离s(km)和甲的行驶时间t(h)的函数关系如图,则下列说法中正确的个数为( )①他们都行使了18千米;
②甲在途中停留了0.5小时;
③乙比甲晚出发了0.5小时;
④甲、乙两人同时到达目的地.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.y=$\sqrt{k-1}$x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
| A. | 没有实数根 | B. | 有一个实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有两个相等的实数根 |
 如图,四边形ABCD为正方形,点E、F在对角线BD上,点G在BC边上,EG⊥AE,GF⊥BD,若BF=3DE,CG=$\sqrt{2}$,则线段AE的长为5.
如图,四边形ABCD为正方形,点E、F在对角线BD上,点G在BC边上,EG⊥AE,GF⊥BD,若BF=3DE,CG=$\sqrt{2}$,则线段AE的长为5.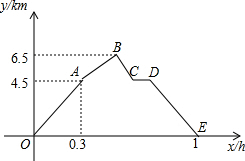 从甲地乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回,途中休息一段时间,小明骑车在平路、上坡、下坡时分别保持匀速前进,上坡的速度比平路上每小时少5km.下坡路的速度比在平路上每小时多5km,设小明出发x(h)后,离开甲地的路面距离为y(km),图中折线OABCDE表示y与x之间的函数关系,则下列说法中正确的个数为( )
从甲地乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回,途中休息一段时间,小明骑车在平路、上坡、下坡时分别保持匀速前进,上坡的速度比平路上每小时少5km.下坡路的速度比在平路上每小时多5km,设小明出发x(h)后,离开甲地的路面距离为y(km),图中折线OABCDE表示y与x之间的函数关系,则下列说法中正确的个数为( )