题目内容
15.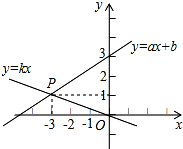 如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )
如图,已知函数y=ax+b和y=kx的图象交于点P,则根据图象可得,关于x、y的二元一次方程组的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-3}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
分析 根据函数图象可以得到两个函数交点坐标,从而可以得到两个函数联立的二元一次方程组的解.
解答 解:根据函数图可知,
函数y=ax+b和y=kx的图象交于点P的坐标是(-3,1),
故$\left\{\begin{array}{l}{y=ax+b}\\{y=kx}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-3}\\{y=1}\end{array}\right.$,
故选C.
点评 本题考查一次函数与二元一次方程组,解题的关键是明确题意,利用数形结合的思想解答问题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.y=$\sqrt{k-1}$x+1是关于x的一次函数,则一元二次方程kx2+2x+1=0的根的情况为( )
| A. | 没有实数根 | B. | 有一个实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有两个相等的实数根 |
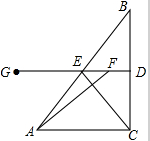 如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在线段BC的垂直平分线DG上,垂足为D,DG交AB于E,连接CE,AF,动点F从D点出发以1cm/s的速度移动,设运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=4cm,动点F在线段BC的垂直平分线DG上,垂足为D,DG交AB于E,连接CE,AF,动点F从D点出发以1cm/s的速度移动,设运动时间为t(s).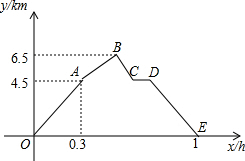 从甲地乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回,途中休息一段时间,小明骑车在平路、上坡、下坡时分别保持匀速前进,上坡的速度比平路上每小时少5km.下坡路的速度比在平路上每小时多5km,设小明出发x(h)后,离开甲地的路面距离为y(km),图中折线OABCDE表示y与x之间的函数关系,则下列说法中正确的个数为( )
从甲地乙地,先是一段平路,然后是一段上坡路,小明骑车从甲地出发,到达乙地后立即原路返回,途中休息一段时间,小明骑车在平路、上坡、下坡时分别保持匀速前进,上坡的速度比平路上每小时少5km.下坡路的速度比在平路上每小时多5km,设小明出发x(h)后,离开甲地的路面距离为y(km),图中折线OABCDE表示y与x之间的函数关系,则下列说法中正确的个数为( ) 尺规作图,不写作法,保留作图痕迹.
尺规作图,不写作法,保留作图痕迹.