题目内容
13. 已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据角平分线的性质、全等三角形的判定定理和性质定理判断即可.
解答 解:∵∠AOC=∠BOC,
∴OC是∠AOB的角平分线,①符合题意;
∵PD⊥OA,PE⊥OB,PD=PE,
∴OC是∠AOB的角平分线,②符合题意;
在Rt△POD和Rt△POE中,
$\left\{\begin{array}{l}{OD=OE}\\{OP=OP}\end{array}\right.$,
∴Rt△POD≌Rt△POE,
∴∠AOC=∠BOC,
∴OC是∠AOB的角平分线,③符合题意;
同理,△POD≌△POE,
∴∠AOC=∠BOC,
∴OC是∠AOB的角平分线,④符合题意,
故选:D.
点评 本题考查的是角平分线的性质、全等三角形的判定和性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.将一张面值为50元的人民币,兑换成10元或20元的零钱,兑换方案有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
4.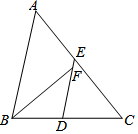 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )| A. | $\frac{5}{8}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | 1.5 |
18.已知等腰三角形的两边长分别为3和6,则它的周长等于( )
| A. | 15 | B. | 12或15 | C. | 12 | D. | 15或18 |
5.若关于x的方程(1-k)x2-2x-1=0有实根,则k的取值范围是( )
| A. | k≥2 | B. | k≤2且k≠1 | C. | k≤2 | D. | k≥2且k≠1 |
2.计算$\frac{x-2}{{x}^{2}}$÷(1-$\frac{2}{x}$)的结果为( )
| A. | $\frac{1}{x}$ | B. | -$\frac{1}{x}$ | C. | x | D. | -$\frac{x-2}{x}$ |
3. 如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
 如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )| A. | $\frac{1}{2}$ | B. | 3 | C. | 2 | D. | 1 |

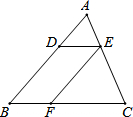 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.