题目内容
4.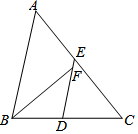 如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )
如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若AB=10,BC=8,则EF的长是( )| A. | $\frac{5}{8}$ | B. | 1 | C. | $\frac{5}{2}$ | D. | 1.5 |
分析 根据三角形中位线定理得到DE∥AB,DE=$\frac{1}{2}$AB=5,根据平行线的性质、角平分线的定义求出DF,计算即可.
解答 解:∵D、E分别是BC、AC的中点,
∴DE∥AB,DE=$\frac{1}{2}$AB=5,BD=$\frac{1}{2}$BC=4,
∴∠ABF=∠BFD,
∵BF平分∠ABC,
∴∠ABF=∠DBF,
∴∠DBF=∠BFD,
∴DF=DB=4,
∴EF=DE-DF=1,
故选:B.
点评 本题考查的是角平分线的定义、三角形中位线定理,掌握平行线的性质、角平分线的定义是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
14. 如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
 如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )
如图,已知AB∥DE,∠C=30°,∠CDE=140°,则∠ABC的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
15.等腰三角形的一个角是80°,则它的底角是( )
| A. | 50° | B. | 80° | C. | 20°或80° | D. | 50°或80° |
12. 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=50°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=50°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=50°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连接AC交⊙O于点D,∠C=50°,点E在AB左侧的半圆上运动(不与A、B重合),则∠AED的大小是( )| A. | 20° | B. | 40° | C. | 50° | D. | 80° |
19.在平面直角坐标系中,函数y=x2-2x的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有( )
| A. | 2个 | B. | 1个或2个或3个 | ||
| C. | 2个或3个或4个 | D. | 1个或2个或3个或4个 |
9.经过一、二、三象限的某一次函数的图象上有A(1,m)、B(-1,n)两点,则( )
| A. | m<0 | B. | n<0 | C. | m+n>0 | D. | m+n>1 |
13. 已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
 已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.一个两位数的个位数字是a,十位数字是b,则这个两位数可表示为( )
| A. | ab | B. | a+b | C. | 10a+b | D. | 10b+a |