题目内容
5.已知a=5,求$\frac{a-4}{{a}^{2}-9}$$÷\frac{1}{a-3}$$•\frac{{a}^{2}+6a+9}{{a}^{2}-8a+16}$的值.分析 先把除法运算化为乘法运算,再把分式的分子分母因式分解得到原式=$\frac{a+3}{a-4}$,然后把a的值代入计算即可.
解答 解:原式=$\frac{a-4}{(a+3)(a-3)}$•(a-3)•$\frac{(a+3)^{2}}{(a-4)^{2}}$
=$\frac{a+3}{a-4}$,
当a=5时,原式=$\frac{5+3}{5-4}$=2.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
16.已知:关于x的方程(m+1)x=n-1无解,则m,n的取值是( )
| A. | m=-1且n=1 | B. | m=-1且n≠1 | C. | m=n=0 | D. | m≠1且n=1 |
 如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.
如图,直线l1∥l2,∠α=∠β,∠1=40°,求∠2的度数.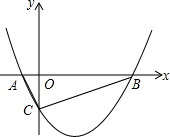 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由. 如图中,BD=2厘米,DE=4厘米,EC=2厘米,F是AE的中点,三角形ABC的BC边上的高是4厘米,阴影面积是多少平方厘米?
如图中,BD=2厘米,DE=4厘米,EC=2厘米,F是AE的中点,三角形ABC的BC边上的高是4厘米,阴影面积是多少平方厘米? 有理数a、b、c在数轴上的位置如图所示,化简:|c|-|b+c|+|c-a|+|b+a|.
有理数a、b、c在数轴上的位置如图所示,化简:|c|-|b+c|+|c-a|+|b+a|.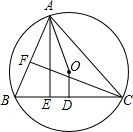 如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).
如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).