题目内容
17.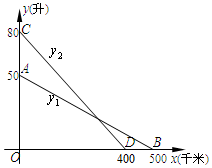 如图,线段AB、CD分别是一辆轿车的油箱剩余油量y1(升)与另一辆客车的油箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.
如图,线段AB、CD分别是一辆轿车的油箱剩余油量y1(升)与另一辆客车的油箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.(1)分别求y1、y2关于x的函数解析式,并写出定义域;
(2)如果两车同时出发,轿车的行驶速度为每小时100千米,客车的行驶速度为每小时80千米,当油箱的剩余油量相同时,两车行驶的时间相差几分钟?
分析 (1)设出线段AB、CD所表示的函数解析式,由待定系数法结合图形可得出结论;
(2)由(1)的结论算出当油箱的剩余油量相同时,跑的路程数,再由时间=路程÷速度,即可得出结论.
解答 解:(1)设AB、CD所表示的函数解析式分别为y1=k1x+50,y2=k2x+80.
结合图形可知:$\left\{\begin{array}{l}{0=500{k}_{1}+50}\\{0=400{k}_{2}+80}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{1}=-0.1}\\{{k}_{2}=-0.2}\end{array}\right.$.
故y1=-0.1x+50(0≤x≤500),y2=-0.2x+80(0≤x≤400).
(2)令y1=y2,则有-0.1x+50=-0.2x+80,
解得:x=300.
轿车行驶的时间为300÷100=3(小时);
客车行驶的时间为300÷80=$3\frac{3}{4}$(小时),
$3\frac{3}{4}$-3=$\frac{3}{4}$小时=45(分钟).
答:当油箱的剩余油量相同时,两车行驶的时间相差45分钟.
点评 本题考查了一次函数的应用,解题的关键:(1)熟练运用待定系数法就解析式;(2)找出剩余油量相同时行驶的距离.本题属于基础题,难度不大,解决该类问题应结合图形,理解图形中点的坐标代表的意义.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
12.做大小两个纸盒,尺规如下(单位:cm)
(1)做这两个纸盒共用料多少平方厘米?(结果用含a、b、c的代数式表示)
(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)
| 长 | 宽 | 高 | |
| 小纸盒 | a | b | c |
| 大纸盒 | 3a | 2b | 2c |
(2)做成的大纸盒比小纸盒的容积大多少立方厘米?(结果用含a、b、c的代数式表示)
2.下列图形中,不一定是轴对称图形的是( )
| A. | 线段 | B. | 等腰三角形 | C. | 四边形 | D. | 圆 |
 有理数a、b、c在数轴上的位置如图所示,化简:|c|-|b+c|+|c-a|+|b+a|.
有理数a、b、c在数轴上的位置如图所示,化简:|c|-|b+c|+|c-a|+|b+a|.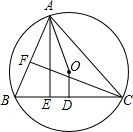 如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).
如图,△ABC内接于⊙O,∠BAC=60°,D是BC的中点,且∠AOD=165°,AE、CF分别是BC、AB边上的高,则∠BAE=22.5(度).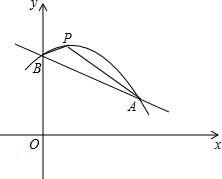 如图,已知抛物线y=-$\frac{1}{8}$x2+bx+c与一次函数y=-$\frac{1}{2}$x+6的图象交于A(8,m)和y轴上的同一点B,P是抛物线的顶点.
如图,已知抛物线y=-$\frac{1}{8}$x2+bx+c与一次函数y=-$\frac{1}{2}$x+6的图象交于A(8,m)和y轴上的同一点B,P是抛物线的顶点. 如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.
如图所示,L1,L2,L3交于点O,∠1=∠2,∠3:∠1=8:1,求∠4的度数.